题目内容
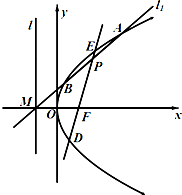 (2013•宁波二模)如图,设抛物线C:y2=2px(p>0)的焦点为F,准线为l,过准线l上一点M(-1,0)且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.
(2013•宁波二模)如图,设抛物线C:y2=2px(p>0)的焦点为F,准线为l,过准线l上一点M(-1,0)且斜率为k的直线l1交抛物线C于A,B两点,线段AB的中点为P,直线PF交抛物线C于D,E两点.(Ⅰ)求抛物线C的方程;
(Ⅱ)若|MA|•|MB|=λ|FD|•|FE|,试写出λ关于k的函数解析式,并求实数λ的取值范围.
分析:(Ⅰ)由题意可得,-
p=-1可求p,进而可求抛物线方程
(Ⅱ)设l1方程为y=k(x+1),A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),
由
整理可得关于y的方程,结合△=16-16k2>0,可求k的范围,然后结合方程的根与系数关系可求y1+y2,y1y2,代入可求x1+x2,x1x2及P,从而可求|MA||MB|及直线PF的方程,由
得关于y的方程,同理可求y3+y4,y3y4,代入直线方程得x3+x4,x3x4,可求|FD||FE|,由题设建立等式,则可以由k表示λ,结合函数的单调性可求λ的范围
| 1 |
| 2 |
(Ⅱ)设l1方程为y=k(x+1),A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),
由
|
|
解答:解:(Ⅰ)-
=-1,p=2,抛物线方程为y2=4x. …(4分)
(Ⅱ)设l1方程为y=k(x+1),A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),
由
得ky2-4y+4k=0,△=16-16k2>0,所以k∈(-1,0)∪(0,1),
y1+y2=
,y1•y2=4,
代入方程得:x1+x2=
-2,x1•x2=1,P(
-1,
)…(6分)
所以|MA|•|MB|=
•
=x1x2+x1+x2+1+y1y2=4(1+
),…(8分)
且直线PF方程为y=
(x-1),
由
得ky2-4(1-k2)y-4k=0,
则得y3+y4=
,y3y4=-4,
代入直线方程得x3+x4=
+2,x3•x4=1,
所以|FD|•|FE|=(x3+1)(x4+1)=
+4,…(10分)
则λ=
,…(12分)
令t=k2+1,则t∈(1,2)λ=
=
而
=
在(1,
)单调递增,在(
,2)单调递减
所以λ∈(1,
] …(14分)
| p |
| 2 |
(Ⅱ)设l1方程为y=k(x+1),A(x1,y1),B(x2,y2),D(x3,y3),E(x4,y4),
由
|
y1+y2=
| 4 |
| k |
代入方程得:x1+x2=
| 4 |
| k2 |
| 2 |
| k2 |
| 2 |
| k |
所以|MA|•|MB|=
| MA |
| MB |
| 1 |
| k2 |
且直线PF方程为y=
| k |
| 1-k2 |
由
|
则得y3+y4=
| 4(1-k2) |
| k |
代入直线方程得x3+x4=
| 4(1-k2)2 |
| k2 |
所以|FD|•|FE|=(x3+1)(x4+1)=
| 4(1-k2)2 |
| k2 |
则λ=
| 1+k2 |
| k4-k2+1 |
令t=k2+1,则t∈(1,2)λ=
| t |
| (t-1)2-t+2 |
| t |
| t2-3t+3 |
而
| t |
| t2-3t+3 |
| 1 | ||
t+
|
| 3 |
| 3 |
所以λ∈(1,
2
| ||
| 3 |
点评:本题主要考查 了利用抛物线的性质求解抛物线的方程及直线与抛物线相交关系的应用,方程的根与系数关系的应用是求解问题的关键

练习册系列答案
相关题目
 (2013•宁波二模)如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3个小组的频数为18,则的值n是
(2013•宁波二模)如图是某学校抽取的n个学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第3个小组的频数为18,则的值n是