题目内容
15.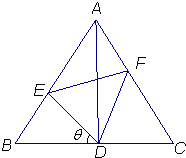 如图,已知△ABC是边长为4的正三角形,D是BC的中点,E,F分别是边AB,AC上的点,且∠EDF=$\frac{π}{3}$,设∠BDE=θ$(\frac{π}{6}<θ<\frac{π}{2})$.
如图,已知△ABC是边长为4的正三角形,D是BC的中点,E,F分别是边AB,AC上的点,且∠EDF=$\frac{π}{3}$,设∠BDE=θ$(\frac{π}{6}<θ<\frac{π}{2})$.(Ⅰ)试将线段DF的长表示为θ的函数;
(Ⅱ)设△DEF的面积为S,求S=f(θ)的解析式,并求f(θ)的最小值;
(Ⅲ)若将折线BE-ED-DF-FC绕直线BC旋转一周得到空间几何体,试问:该几何体的体积是否有最小值?若有,求出它的最小值;若没有,请说明理由.
分析 (Ⅰ)根据正弦定理求出即可;
(Ⅱ)根据正弦定理求出DE,表示出三角形的面积,结合角的范围,从而求出三角形的最小值;
(Ⅲ)先求出组合体的体积,根据基本不等式的性质,解出答案.
解答 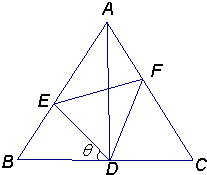 解:(Ⅰ)在△DFC中,∠FDC=$\frac{2π}{3}$-θ,∠C=$\frac{π}{3}$,∠DFC=θ,
解:(Ⅰ)在△DFC中,∠FDC=$\frac{2π}{3}$-θ,∠C=$\frac{π}{3}$,∠DFC=θ,
由正弦定理:$\frac{DF}{sinC}$=$\frac{DC}{sinθ}$,得$\frac{DF}{sin\frac{π}{3}}$=$\frac{2}{sinθ}$,
即DF=$\frac{\sqrt{3}}{sinθ}$($\frac{π}{6}$<θ<$\frac{π}{2}$),
(Ⅱ)在△BDE中,∠BED=$\frac{2π}{3}$-θ,∠B=$\frac{π}{3}$,∠BDE=θ,
由正弦定理:$\frac{BD}{sin∠BED}$=$\frac{DE}{sinB}$,得:DE=$\frac{BDsinB}{sin∠BED}$=$\frac{\sqrt{3}}{sin(\frac{2π}{3}-θ)}$,
∴S=$\frac{1}{2}$DE•DF•sin$\frac{π}{3}$=$\frac{\sqrt{3}}{4}$•$\frac{\sqrt{3}}{sin(\frac{2π}{3}-θ)}$•$\frac{\sqrt{3}}{sinθ}$=$\frac{3\sqrt{3}}{2sin(2θ-\frac{π}{6})+1}$,
∵θ∈($\frac{π}{6}$,$\frac{π}{2}$),∴2θ-$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{5π}{6}$),
当2θ-$\frac{π}{6}$=$\frac{π}{2}$,即θ=$\frac{π}{3}$时,Smin=$\frac{3\sqrt{3}}{2+1}$=$\sqrt{3}$;
(Ⅲ)存在,最小值为4π,理由如下:
该几何体是由四个圆锥构成的组合体,过E点作EM⊥BD于M点,则EM=EDsinθ,
过F点作FN⊥DC于N点,则FN=DFsin($\frac{2π}{3}$-θ),
EM•FN=$\frac{\sqrt{3}}{sin(\frac{2π}{3}-θ)}$sinθ•$\frac{\sqrt{3}}{sinθ}$sin($\frac{2π}{3}$-θ)=3,
则组合体的体积V=$\frac{1}{3}$π•EM2•BD+$\frac{1}{3}$π•FN2•DC=$\frac{2π}{3}$(EM2+FN2),
所以V≥$\frac{2π}{3}$•2EM•FN=4π,当且仅当EM=FN时取“=”,
所以所得几何体的体积有最小值为4π.
点评 本题考查了解三角形问题,考查函数最值问题,考查基本不等式的性质的应用,是一道中档题.

| x | 1 | 2 | 3 | 4 |
| y | 17 | 12 | 7 | 4 |
| A. | a>0,b>0 | B. | a>0,b<0 | C. | a<0,b>0 | D. | a<0,b>0 |
| A. | 4 | B. | 1 | C. | -4 | D. | -1 |
| A. | 10种 | B. | 20种 | C. | 30种 | D. | 40种 |
| A. | (0,3] | B. | [-1,3] | C. | (-∞,-1)∪[3,+∞) | D. | (-∞,1]∪[3,+∞) |
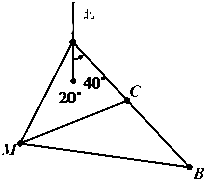 如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?
如图,已知点M在A城的南偏西20°的方向上,现有一辆汽车在点B沿公路向A城行驶,公路的走向是A城的南偏东40°.开始时,汽车到M的距离为31km,汽车前进20km到达点C时,到M的距离缩短了10km,问汽车还要行驶多远才能到达A城?