题目内容
【题目】已知椭圆C的两个焦点分别为F1（﹣ 
，0），F2（ ，0），且椭圆C过点P（3，2）．
（1）求椭圆C的标准方程；
（2）与直线OP平行的直线交椭圆C于A，B两点，求△PAB面积的最大值．
【答案】
（1）解：由题意设椭圆方程为 
=1，
∵椭圆C的两个焦点分别为F1（﹣ 
，0），
F2（ ，0），且椭圆C过点P（3，2），
由椭圆定义可得2a= 
+ 
=6 
，即a=3 ，
∴b2=a2﹣c2=8，
则椭圆C的标准方程为 
=1；
（2）解：由kOP= 
，
设与直线OP平行的直线方程为y= x+m，
联立 
，得8x2+12mx+9m2﹣72=0．
由判别式△=144m2﹣32（9m2﹣72）＞0，解得0＜|m|＜4．
设A（x1，y1），B（x2，y2），则x1+x2=﹣ 
m，x1x2= 
，
|AB|= 
= 
，
点O到直线AB的距离为d= 
= 
|m|，
即有△PAB面积为S= 
|AB|d= 
= 
≤ 
=6．
当且仅当9m2=144﹣9m2，即m=±2 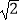时，取得最大值6．
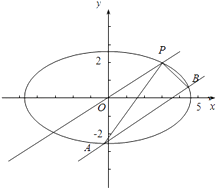
【解析】（1）由题意设椭圆方程为 =1，利用椭圆定义求得a，结合隐含条件求得b，则椭圆方程可求；（2）求出kOP= ，设与直线OP平行的直线方程为y= x+m，联立直线和椭圆方程，运用韦达定理和判别式大于0，以及弦长公式，点到直线的距离公式和三角形的面积公式，结合基本不等式即可得到所求最大值．
练习册系列答案
相关题目
