题目内容
【题目】已知函数 .
.
(I)求![]() ,
,![]() 的值;
的值;
(II)求![]() ;
;
(III)若![]() ,求
,求![]() .
.
【答案】(I)![]() ,-11 ; (II)f(8x﹣1)=
,-11 ; (II)f(8x﹣1)=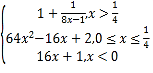 ;(III)
;(III)![]() 或
或![]()
【解析】
(I)根据函数的解析式依次求值即可;(II)根据解析式对8x﹣1分三种情况依次求出,最后再用分段函数的形式表示出f(8x﹣1);(III)根据解析式对4a分三种情况,分别由条件列出方程求出a的值.
(I)由题意得,![]() f(1+
f(1+![]() )=f(2+
)=f(2+![]() )=1+
)=1+![]()
=1+![]() ,
,
又f(﹣4)=﹣8+3=-5,则f(-5)=-10+3=-7,f(-7)=-14+3=-11,
所以![]() ;
;
(II)当8x﹣1>1即x>![]() 时,f(8x﹣1)=1+
时,f(8x﹣1)=1+![]() ,
,
当﹣1≤8x﹣1≤1即0≤x≤![]() 时,f(8x﹣1)=(8x﹣1)2+1=64x2﹣16x+2,
时,f(8x﹣1)=(8x﹣1)2+1=64x2﹣16x+2,
当8x﹣1<﹣1即x<0时,f(8x﹣1)=2(8x﹣1)+3=16x+1,
综上可得,f(8x﹣1)=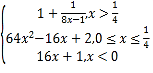 ;
;
(III)因为![]() ,所以分以下三种情况:
,所以分以下三种情况:
当4a>1时,即a>![]() 时,f(4a)=
时,f(4a)=![]() =
=![]() ,解得a=
,解得a=![]() ,成立,
,成立,
当﹣1≤4a≤1时,即-![]() ≤a≤
≤a≤![]() 时,f(4a)=16a2+1=
时,f(4a)=16a2+1=![]() ,解得a=
,解得a=![]() ,成立
,成立
当4a<﹣1时,即a<-![]() 时,f(4a)=8a+3=
时,f(4a)=8a+3=![]() ,解得a=-
,解得a=-![]() ,不成立,
,不成立,
综上可得,a的值是![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目