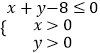题目内容
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)讨论函数![]() 的单调性;
的单调性;
(2)函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,
两点, ![]() ,点
,点![]() 在函数
在函数![]() 的图象上,且
的图象上,且![]() 为等腰直角三角形,记
为等腰直角三角形,记 ,求
,求![]() 的值.
的值.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)对函数求导,利用导数与函数单调性的关系,对![]() 进行分类讨论可得结果;(2)由函数图象交
进行分类讨论可得结果;(2)由函数图象交![]() 轴于两点,两点横坐标满足方程.又根据直角三角斜边的中线性质可得
轴于两点,两点横坐标满足方程.又根据直角三角斜边的中线性质可得![]() 三者间关系,最后利用
三者间关系,最后利用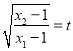 将方程转化成只含有
将方程转化成只含有![]() 两个变量,可求得两变量关系,进一步求得
两个变量,可求得两变量关系,进一步求得![]() 的值.试题解析:
的值.试题解析:
(Ⅰ)![]() .
.
①当![]() 时,则
时,则![]() ,则函数
,则函数![]() 在
在![]() 是单调增函数.
是单调增函数.
②当![]() 时,令
时,令![]() ,则
,则![]() ,
,
若![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 上是单调减函数;
上是单调减函数;
若![]() ,
, ![]() ,所以
,所以![]() 在
在![]() 上是单调增函数.
上是单调增函数.
(Ⅱ)由(Ⅰ)可知当![]() 时,函数
时,函数![]() 其图象与
其图象与![]() 轴交于两点,则有
轴交于两点,则有![]() ,则
,则![]()
![]()
![]() .
.
于是![]() ,在等腰三角形ABC中,显然C = 90°,所以
,在等腰三角形ABC中,显然C = 90°,所以![]() ,即
,即![]() ,
,
由直角三角形斜边的中线性质,可知![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
即![]() .
.
因为![]() ,则
,则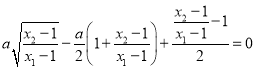 ,
,
又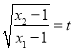 ,所以
,所以![]() ,
,
即![]() ,则
,则![]() 所以
所以![]() .
.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差![]() (单位:分)与物理偏差
(单位:分)与物理偏差![]() (单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差 | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差 | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: 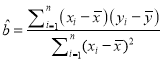 ,
, ![]() ,
,
参考数据: ![]() ,
, ![]() .
.
【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查![]() 人,并将调查情况进行整理后制成下表:
人,并将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
频数 |
|
|
|
|
|
赞成人数 |
|
|
|
|
|
(1)世界联合国卫生组织规定: ![]() 岁为青年,
岁为青年, ![]() 为中年,根据以上统计数据填写以下
为中年,根据以上统计数据填写以下![]() 列联表:
列联表:
青年人 | 中年人 | 合计 | |
不赞成 | |||
赞成 | |||
合计 |
(2)判断能否在犯错误的概率不超过![]() 的前提下,认为赞成“车柄限行”与年龄有关?
的前提下,认为赞成“车柄限行”与年龄有关?
附: 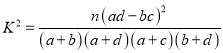 ,其中
,其中![]()
独立检验临界值表:
|
|
|
|
|
|
|
|
|
|
(3)若从年龄![]() 的被调查中各随机选取
的被调查中各随机选取![]() 人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为
人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.