题目内容
函数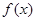 的定义域为R,
的定义域为R,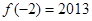 ,对任意
,对任意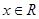 ,都有
,都有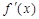 <
<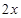 成立,则不等式
成立,则不等式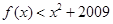 的解集为( )
的解集为( )
| A.(-2,2) | B.(-2,+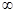 ) ) | C.(-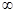 ,-2) ,-2) | D.(-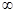 ,+ ,+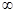 ) ) |
C
解析试题分析:构造函数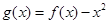 ,因为,对任意
,因为,对任意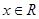 ,都有
,都有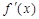 <
<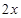 成立,
成立,
即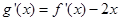 <0成立,所以函数
<0成立,所以函数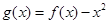 是减函数。
是减函数。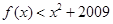 ,即
,即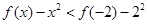 ,故
,故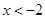 ,选C。
,选C。
考点:利用导数研究函数的单调性,抽象不等式的解法。
点评:中档题,本题关键是构造函数,通过研究函数的单调性,达到解不等式的目的。

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
定义:符合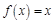 的
的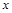 称为
称为 的一阶不动点,符合
的一阶不动点,符合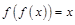 的
的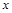 称为
称为 的二阶不动点。设函数
的二阶不动点。设函数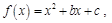 若函数
若函数 没有一阶不动点,则函数
没有一阶不动点,则函数 二阶不动点的个数为 ( )
二阶不动点的个数为 ( )
| A.四个 | B.两个 | C.一个 | D.零个 |
函数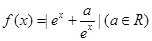 在区间
在区间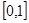 上单调递增,则
上单调递增,则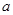 的取值范围是( )
的取值范围是( )
A.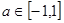 | B.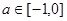 | C.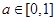 | D.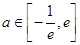 |
曲线y=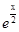 在点(4,
在点(4,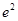 )处的切线与坐标轴所围成的三角形的面积为
)处的切线与坐标轴所围成的三角形的面积为
A.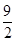 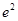 | B.4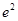 | C.2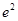 | D.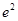 |
若函数 的导函数
的导函数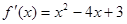 ,则使得函数
,则使得函数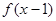 单调递减的一个充分不必要条件是
单调递减的一个充分不必要条件是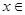 ( )
( )
| A.(0,1) | B.[0,2] | C.(2,3) | D.(2,4) |
设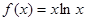 ,若
,若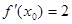 ,则
,则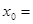 ( )
( )
A.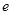 | B.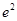 | C.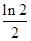 | D.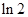 |
函数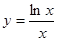 的最大值为( )
的最大值为( )
A. | B.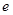 | C.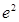 | D.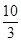 |
已知函数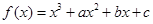 有两个极值点
有两个极值点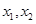 ,若
,若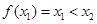 ,则关于
,则关于 的方程
的方程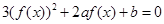 的不同实根个数为
的不同实根个数为
| A.3 | B. 4 |
| C.5 | D. 6 |
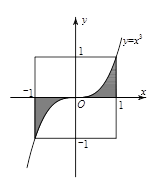
 是图中边长为2的正方形区域,
是图中边长为2的正方形区域,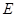 是函数
是函数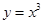 的图象与
的图象与 轴及
轴及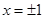 围成的阴影区域.向
围成的阴影区域.向