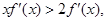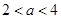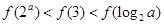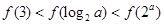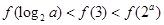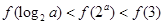题目内容
若函数 的导函数
的导函数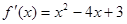 ,则使得函数
,则使得函数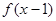 单调递减的一个充分不必要条件是
单调递减的一个充分不必要条件是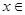 ( )
( )
| A.(0,1) | B.[0,2] | C.(2,3) | D.(2,4) |
C
解析试题分析:因为,函数 的导函数
的导函数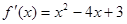 ,
,
所以,x>3或x<1时,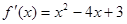 >0,函数为增函数;
>0,函数为增函数;
1<x<3时,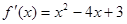 <0,函数为减函数,
<0,函数为减函数,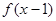 的单调区间,是
的单调区间,是 的单调区间,向右平移1个单位,所以,其减区间为(2,4),使得函数
的单调区间,向右平移1个单位,所以,其减区间为(2,4),使得函数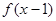 单调递减的一个充分不必要条件是
单调递减的一个充分不必要条件是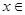 (2,3),选C。
(2,3),选C。
考点:利用导数研究函数的单调性,充要条件的概念。
点评:小综合题,在给定区间,导函数值非负,函数为增函数;导函数值非正,函数为减函数。涉及充要条件问题,可以利用“定义法、等价关系法、集合关系法”加以判断。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数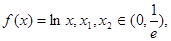 且
且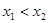 则下列结论正确的是( )
则下列结论正确的是( )
A.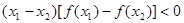 | B.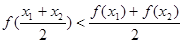 |
C.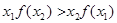 | D.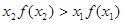 |
设函数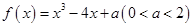 有三个零点
有三个零点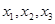 ,且
,且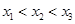 则下列结论正确的是( )
则下列结论正确的是( )
A.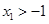 | B.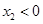 | C.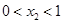 | D.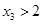 |
已知二次函数 的导数
的导数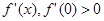 ,且
,且 的值域为
的值域为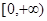 ,则
,则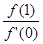 的最小值为( )
的最小值为( )
| A.3 | B.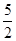 | C.2 | D.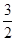 |
函数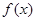 的定义域为R,
的定义域为R,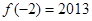 ,对任意
,对任意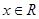 ,都有
,都有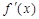 <
<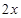 成立,则不等式
成立,则不等式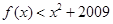 的解集为( )
的解集为( )
| A.(-2,2) | B.(-2,+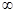 ) ) | C.(-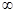 ,-2) ,-2) | D.(-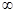 ,+ ,+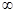 ) ) |
对于R上的可导的任意函数 ,若满足
,若满足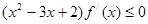 ,则函数
,则函数 在区间
在区间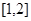 上必有( )
上必有( )
A. | B.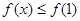 |
C.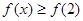 | D.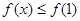 或 或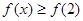 |
设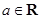 ,函数
,函数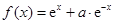 的导函数是
的导函数是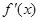 ,且
,且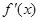 是奇函数.若曲线
是奇函数.若曲线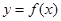 的一条切线的斜率是
的一条切线的斜率是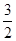 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.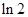 | B.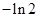 | C.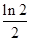 | D.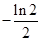 |
已知曲线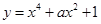 在点
在点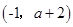 处切线的斜率为8,
处切线的斜率为8,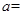 ( )
( )
A.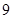 | B.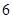 | C.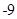 | D.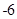 |
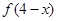
 ,且当
,且当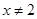
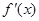 满足
满足