题目内容
若n的展开式中前三项的系数成等差数,则展开式中x4项的系数为( )
| A.6 | B.7 |
| C.8 | D.9 |
B
分析:求出)n的展开式中前三项的系数Cn0、

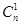 、
、
 , 由等差数列知识求出n,再利用通项公式求出x4项的系数即可.
, 由等差数列知识求出n,再利用通项公式求出x4项的系数即可.解:因为n的展开式中前三项的系数Cn0、

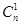 、
、
 成等差数列,
成等差数列,所以
 +
+
 =
=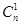 ,即n2-9n+8=0,解得:n=8或n=1(舍).
,即n2-9n+8=0,解得:n=8或n=1(舍).Tr+1=
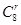 x8-r(
x8-r(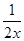 )r=(
)r=( )r
)r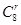 x8-2r.
x8-2r.令8-2r=4可得,r=2,所以x4的系数为(
 )2
)2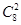 =7,
=7,故选B

练习册系列答案
相关题目
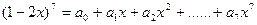
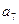 ; (2)
; (2)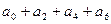 .
. 如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有 种(用数字作答).
如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有 种(用数字作答). 乓球、篮球、足球运动队,每人限报一项,不同的报名方法的种数是
乓球、篮球、足球运动队,每人限报一项,不同的报名方法的种数是