题目内容
1.在△ABC中,内角A,B,C的对边分别为a,b,c,且(b+c)2-a2=tan75°bc(Ⅰ)求cosA的值;
(Ⅱ)若a=2,求$\overrightarrow{BA}$•$\overrightarrow{BC}$的取值范围;
(Ⅲ)若b=2,求$\overrightarrow{BA}$•$\overrightarrow{BC}$的取值范围.
分析 (Ⅰ)由已知得到tan75°,得到a2=b2+c2-$\sqrt{3}$bc,利用余弦定理解得;
(Ⅱ)由a=2,A=30°,得△ABC外接圆直径2R=4,且点A在优弧上任意运动.设有向线段BD长为x,则$\overrightarrow{BA}$•$\overrightarrow{BC}$=2x,由x范围求得;
(Ⅲ)设线段AC中点为D,由图可知|BD|∈[$\frac{1}{2}$,+∞).而$\overrightarrow{BA}$•$\overrightarrow{BC}$用BD表示得到所求.
解答 解:(Ⅰ)因为:tan75°=tan(45°+30°)=$\frac{1+\frac{\sqrt{3}}{3}}{1-\frac{\sqrt{3}}{3}}=2+\sqrt{3}$,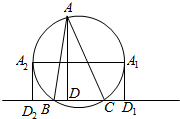
所以:(b+c)2-a2=tan75°bc,展开后得:a2=b2+c2-$\sqrt{3}$bc
故cosA=$\frac{\sqrt{3}}{2}$,即A=30°…(4分)
(II)由a=2,A=30°,得△ABC外接圆直径2R=4,且点A在优弧上任意运动.
由图:AD⊥BC于点D,设有向线段BD长为x,则$\overrightarrow{BA}$•$\overrightarrow{BC}$=2x,
由图可知:x∈[-1,3],故$\overrightarrow{BA}$•$\overrightarrow{BC}$∈[-2,6]…(8分)
(III)设线段AC中点为D,AC=2,由图可知|BD|∈[$\sqrt{3}$,+∞).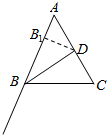
由:$\overrightarrow{BA}$•$\overrightarrow{BC}$=$\frac{1}{4}$[($\overrightarrow{BA}$+$\overrightarrow{BC}$)2-($\overrightarrow{BA}$-$\overrightarrow{BC}$)2]=|BD|2-1,
所以:$\overrightarrow{BA}$•$\overrightarrow{BC}$∈[2,+∞).…(12分)
点评 本题考查了余弦定理的运用、向量的数量积范围等知识,属于中档题.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案| A. | 归纳推理 | B. | 类比推理 | C. | 演绎推理 | D. | 以上均有可能 |
| 认为作业多 | 认为作业不多 | 总数 | |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
附:
| P(K2》k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
| A. | 99% | B. | 95% | C. | 90% | D. | 无充分依据 |
| A. | a>ab>ab2 | B. | ab>a>ab2 | C. | ab>ab2>a | D. | ab2>ab>a |
 将一个长宽分别为2米和2k米(0<k<1)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,记切去的正方形边长为x(0<x<k),
将一个长宽分别为2米和2k米(0<k<1)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,记切去的正方形边长为x(0<x<k),