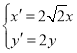题目内容
【题目】已知![]() (
(![]() 是实数,方程
是实数,方程![]() 有两个实根
有两个实根![]() ,数列
,数列![]() 满足
满足![]() (
(![]() ).
).
(1)求数列![]() 的通项公式(用
的通项公式(用![]() 表示);
表示);
(2)若![]() ,求
,求![]() 的前
的前![]() 项和.
项和.
【答案】![]() ,
,![]()
【解析】
方法一:
(Ⅰ)由韦达定理知![]() ,又
,又![]() ,所以
,所以
![]() ,
,![]()
整理得![]()
令![]() ,则
,则![]() .所以
.所以![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
数列![]() 的首项为:
的首项为:
![]() .
.
所以![]() ,即
,即![]()
![]() .所以
.所以![]()
![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,
,![]()
![]() 变为
变为![]()
![]() .整理得,
.整理得,![]() ,
,![]() .所以,数列
.所以,数列![]() 成公差为
成公差为![]() 的等差数列,其首项为
的等差数列,其首项为![]() .所以
.所以
![]() .
.
于是数列![]() 的通项公式为
的通项公式为
![]() ;……………………………………………………………………………5分
;……………………………………………………………………………5分
②当![]() 时,
时,![]() ,
,
![]()
![]()
![]()
![]() .
.
整理得
![]() ,
,![]() .
.
所以,数列![]() 成公比为
成公比为![]() 的等比数列,其首项为
的等比数列,其首项为![]() .所以
.所以![]() .
.
于是数列![]() 的通项公式为
的通项公式为![]() .………………………………………………10分
.………………………………………………10分
(Ⅱ)若![]() ,
,![]() ,则
,则![]() ,此时
,此时![]() .由第(Ⅰ)步的结果得,数列
.由第(Ⅰ)步的结果得,数列![]() 的通项公式为
的通项公式为![]() ,所以,
,所以,![]() 的前
的前![]() 项和为
项和为
![]()
![]()
以上两式相减,整理得![]()
所以![]() .……………………………………………………………………………15分
.……………………………………………………………………………15分
方法二:
(Ⅰ)由韦达定理知![]() ,又
,又![]() ,所以
,所以
![]() ,
,![]() .
.
特征方程![]() 的两个根为
的两个根为![]() ,
,![]() .
.
①当![]() 时,通项
时,通项![]() 由
由![]() ,
,![]() 得
得
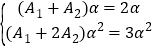
解得![]() .故
.故![]() .……………………………………………………5分
.……………………………………………………5分
②当![]() 时,通项
时,通项![]() .由
.由![]() ,
,![]() 得
得
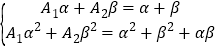
解得![]() ,
,![]() .故
.故
![]() .…………………………………………………………10分
.…………………………………………………………10分
(Ⅱ)同方法一.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目