题目内容
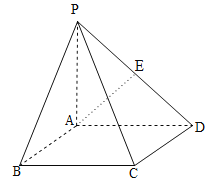
【题目】如图,有一块三棱锥形木块![]() ,各面均是锐角三角形,其中面
,各面均是锐角三角形,其中面![]() 内有一点
内有一点![]() .
.
(1)若要在面![]() 内过点
内过点![]() 画一条线段
画一条线段![]() ,其中点
,其中点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() 与
与![]() 垂直,该如何求作?请在图中画出线段
垂直,该如何求作?请在图中画出线段![]() 并说明画法,不必证明;
并说明画法,不必证明;
(2)经测量,![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() 恰为三角形
恰为三角形![]() 的重心,
的重心,![]() 为(1)中所求线段,求三棱锥
为(1)中所求线段,求三棱锥![]() 的体积.
的体积.
【答案】(1)作图详见解析;(2)![]() .
.
【解析】
(1)先在![]() 上任取一点
上任取一点![]() ,分别在平面
,分别在平面![]() 和平面
和平面![]() 内作
内作![]() 的垂线分交
的垂线分交![]() 、
、![]() 于点
于点![]() 、
、![]() ,可得出
,可得出![]() 平面
平面![]() ,进而得出
,进而得出![]() ,然后分两种情况讨论,
,然后分两种情况讨论,![]() 和
和![]() ,即可作出
,即可作出![]() ;
;
(2)先证明出![]() ,根据重心的性质得出三棱锥
,根据重心的性质得出三棱锥![]() 的体积为三棱锥
的体积为三棱锥![]() 体积的
体积的![]() ,利用余弦定理计算出
,利用余弦定理计算出![]() 、
、![]() ,进而计算出
,进而计算出![]() 的面积,由此可计算出三棱锥
的面积,由此可计算出三棱锥![]() 的体积,进而得出三棱锥
的体积,进而得出三棱锥![]() 的体积.
的体积.
(1)如图,在![]() 上任取一点
上任取一点![]() ;
;
过点![]() 在平面
在平面![]() 内作
内作![]() 的垂线,交
的垂线,交![]() 于
于![]() ;
;
过点![]() 在平面
在平面![]() 内作
内作![]() 的垂线,交
的垂线,交![]() 于
于![]() .
.
连接![]() ,若
,若![]() 过点
过点![]() ,则
,则![]() 就是所求线段
就是所求线段![]() ;
;
若![]() 不过点
不过点![]() ,则过点
,则过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 、
、![]() 相交即得线段
相交即得线段![]() .
.
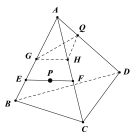
(2)取![]() 中点
中点![]() ,连
,连![]() 、
、![]() ,
,
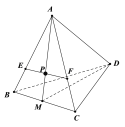
因为![]() 为三角形
为三角形![]() 的重心,故
的重心,故![]() 在
在![]() 上,且
上,且![]() .
.
由题意知,![]() ,
,![]() ,
,![]() ,故
,故![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() 与
与![]() 共面,于是
共面,于是![]() ,
,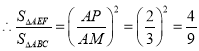 ,
,
故三棱锥![]() 的体积为三棱锥
的体积为三棱锥![]() 体积的
体积的![]() .
.
![]() ,
,![]() ,则
,则![]() 为等边三角形,
为等边三角形,![]() ,
,
![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
整理得![]() ,解得
,解得![]() 或
或![]() .
.
若![]() ,此时
,此时![]() 为等腰三角形,
为等腰三角形,![]() ,
,![]() ,合乎题意;
,合乎题意;
若![]() ,则
,则![]() ,
,![]() 为钝角,不合乎题意.
为钝角,不合乎题意.
同理可得![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,由余弦定理得
,由余弦定理得![]() ,
,
![]() ,
,![]() ,
,
故![]() .
.

练习册系列答案
相关题目