题目内容
正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点.则:
(1)二面角E-AB-C的平面角的正切值是
;
(2)二面角C-AE-B的平面角的正切值是
(3)点D1到平面EAB的距离是
.
(1)二面角E-AB-C的平面角的正切值是
| 1 |
| 2 |
| 1 |
| 2 |
(2)二面角C-AE-B的平面角的正切值是
3
3
;(3)点D1到平面EAB的距离是
2
| ||
| 5 |
2
| ||
| 5 |
分析:(1)由正方体性质,AB⊥面EBC,∴AB⊥BC,AB⊥EB,∴∠EBC二面角E-AB-C的平面角
(2)连接BD交AC于O,过点O作OF⊥AE交AE于F,连接OF,可得∠OFB是二面角C-AE-B的平面角.根据相似三角形性质求出OF后,解三角形BOF即可.
(3)由于D1C1∥平面ABE,即D1到平面ABE的距离等于C1到平面ABE的距离,利用等体积法求出C1到平面ABE的距离即可.
(2)连接BD交AC于O,过点O作OF⊥AE交AE于F,连接OF,可得∠OFB是二面角C-AE-B的平面角.根据相似三角形性质求出OF后,解三角形BOF即可.
(3)由于D1C1∥平面ABE,即D1到平面ABE的距离等于C1到平面ABE的距离,利用等体积法求出C1到平面ABE的距离即可.
解答:解(1)由正方体性质,AB⊥面EBC,∴AB⊥BC,AB⊥EB,∴∠EBC二面角E-AB-C的平面角
在直角三角形ECB中,tan∠EBC=
=
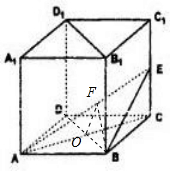
(2)连接BD交AC于O,过点O作OF⊥AE交AE于F,连接OF
∵BO⊥平面ACE,∴AE⊥AE,∴AE⊥面OFB,AE⊥BF,∴∠OFB是二面角C-AE-B的平面角.
在直角三角形ACE中,AC=2
,AO=
,AE=3,∵OF:CE=AO:AE,∴OF=
,
在直角三角形FOB中,tan∠OFB=
=3.
(3)D1C1∥平面ABE,∴点C1到平面EAB的距离等于点D1到平面EAB的距离 h.
∴V A-BCE1=V C1-ABE 即
S△BEC1×AB=
△ABE×h,
又S△BEC1=
×2×1=1.S△ABE=
×AB×BE=
×2×
=
.
∴
× 1×2=
×
× h,h=
.
在直角三角形ECB中,tan∠EBC=
| EC |
| BC |
| 1 |
| 2 |

(2)连接BD交AC于O,过点O作OF⊥AE交AE于F,连接OF
∵BO⊥平面ACE,∴AE⊥AE,∴AE⊥面OFB,AE⊥BF,∴∠OFB是二面角C-AE-B的平面角.
在直角三角形ACE中,AC=2
| 2 |
| 2 |
| ||
| 3 |
在直角三角形FOB中,tan∠OFB=
| OB |
| OF |
(3)D1C1∥平面ABE,∴点C1到平面EAB的距离等于点D1到平面EAB的距离 h.
∴V A-BCE1=V C1-ABE 即
| 1 |
| 3 |
| 1 |
| 3 |
又S△BEC1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
2
| ||
| 5 |
点评:本题考查的知识点是二面角的平面角及求法,点到平面的距离,(1)的关键是利用定义直接找出所求的二面角的平面角,(2)的关键是通过作垂线,确定∠OFB是二面角B-AE-C的平面角,(3)的关键是转化成C1到平面ABE的距离.考查空间想象、转化、计算能力.

练习册系列答案
相关题目
 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的: 已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点. 如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.
如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积. 如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )
如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )