题目内容
 如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )
如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )分析:先做B1E⊥平面A1MC与E,根据DC∥A1B1得到∠B1A1E为所求;然后通过体积相等求出B1E的长,即可求出答案.
解答: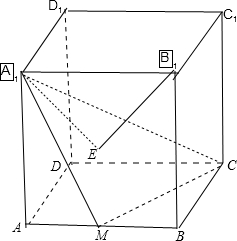 解:做B1E⊥平面A1MC与E
解:做B1E⊥平面A1MC与E
设B1E=h
∵DC∥A1B1,则∠B1A1E为所求的线面角;
设此正方体所有棱边长为1.
如图,因为M是棱AB的中点,
所以:CM=
=
,同理A1M=
,
而CA1=
AB=
.
∴在等腰三角形A1MC中底边A1C边上的高为
.
∴S△A1MC=
×
×
=
;
∵VB1-A1MC=VC-A1B1 M
∴
•h•S△A1MC=
•BC•S△A1B1C
∴
•h•
=
×1×
×1×1⇒h=
=
.
∴sin∠B1A1E=
=
.
即过A1,M,C三点的平面与CD所成角正弦值为:
.
故选:D.
 解:做B1E⊥平面A1MC与E
解:做B1E⊥平面A1MC与E设B1E=h
∵DC∥A1B1,则∠B1A1E为所求的线面角;
设此正方体所有棱边长为1.
如图,因为M是棱AB的中点,
所以:CM=
| CB 2+AM 2 |
| ||
| 2 |
| ||
| 2 |
而CA1=
| 3 |
| 3 |
∴在等腰三角形A1MC中底边A1C边上的高为
| ||
| 2 |
∴S△A1MC=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 4 |
∵VB1-A1MC=VC-A1B1 M
∴
| 1 |
| 3 |
| 1 |
| 3 |
∴
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 | ||
|
| ||
| 3 |
∴sin∠B1A1E=
| B1E |
| A1B1 |
| ||
| 3 |
即过A1,M,C三点的平面与CD所成角正弦值为:
| ||
| 3 |
故选:D.
点评:本题主要考察直线与平面所成的角.解决本题的关键在于通过DC∥A1B1把问题转化为求∠B1A1E.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目

 如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量
如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG. 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( ) 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且