题目内容
 如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.
如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.分析:根据线面平行的定义和性质可以证明与截面PBC1平行的截面是平行四边形.然后求平行四边形的面积即可.
解答:解:取AB、C1D1的中点M、N,连结A1M、MC、CN、NA1.
由于A1N∥PC1∥MC且A1N=PC1=MC,
∴四边形A1MCN是平行四边形.
又∵A1N∥PC1,A1M∥BP,A1N∩A1M=A1,
PC1∩BP=P,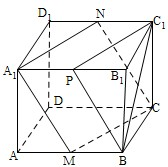
∴平面A1MCN∥平面PBC1
因此,过A1点作与截面PBC1平行的截面是平行四边形.
又连结MN,作A1H⊥MN于H,由于A1M=A1N=
,MN=2
,
则AH=
.
∴S△A1MN=
×2
×
=
故 S平行四边形A1MCN=2S△A1MN=2
(cm2).
由于A1N∥PC1∥MC且A1N=PC1=MC,
∴四边形A1MCN是平行四边形.
又∵A1N∥PC1,A1M∥BP,A1N∩A1M=A1,
PC1∩BP=P,

∴平面A1MCN∥平面PBC1
因此,过A1点作与截面PBC1平行的截面是平行四边形.
又连结MN,作A1H⊥MN于H,由于A1M=A1N=
| 5 |
| 2 |
则AH=
| 3 |
∴S△A1MN=
| 1 |
| 2 |
| 2 |
| 3 |
| 6 |
故 S平行四边形A1MCN=2S△A1MN=2
| 6 |
点评:本题主要考查空间立体几何中截面的形状的判断,利用线面平行或面面平行的定义和性质是解决本题的关键.

练习册系列答案
相关题目
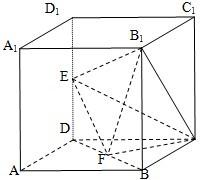 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.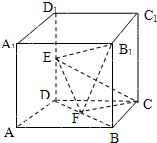 17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点
17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点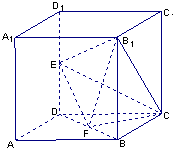 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 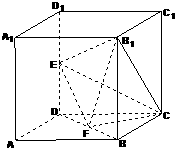 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.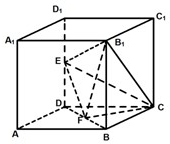 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.