题目内容
2.已知f(x)为奇函数,当x≥0时,f(x)=2x+t,f(m)<3,则m取值范围是m<2.分析 根据奇函数的结论:f(0)=0求出t,设x<0则-x>0,利用奇函数的性质求出函数f(x)的解析式,利用分类讨论求出f(m)<3时,m的取值范围.
解答 解:∵f(x)是定义在R上的奇函数,当x≥0时f(x)=2x+t(t为常数),
∴f(0)=20+t=0,解得t=-1,
则当x≥0时,f(x)=2x-1,
设x<0,则-x>0,
∴f(x)=-f(-x)=-(2-x-1)=-2-x+1,
又f(m)<3,
∴$\left\{\begin{array}{l}{m≥0}\\{{2}^{m}-1<3}\end{array}\right.$或$\left\{\begin{array}{l}{m<0}\\{-{2}^{-m}+1<3}\end{array}\right.$,
∴m<2.
故答案为:m<2.
点评 本题考查利用函数的奇偶性求函数的解析式,充要条件的判断,以及分类讨论求不等式的解集,属于中档题.

练习册系列答案
相关题目
10.已知直线y=kx-2k-1与直线x+2y-4=0的交点位于第一象限,则k的取值范围是( )
| A. | -$\frac{3}{2}$<k<$\frac{1}{2}$ | B. | k>$\frac{1}{2}$或k<-$\frac{3}{2}$ | C. | k≥$\frac{1}{2}$或k≤-$\frac{3}{2}$ | D. | k>-$\frac{1}{6}$ |
14.已知函数f(x)=sinx+x2013,令f1(x)=f′(x),f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),则f2014(x)=( )
| A. | -sinx | B. | -sinx+x | C. | cosx | D. | cosx+x |
11.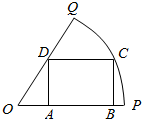 如图所示,扇形OPQ的半径为2,圆心角为$\frac{π}{3}$,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,则SABCD的最大值是( )
如图所示,扇形OPQ的半径为2,圆心角为$\frac{π}{3}$,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,则SABCD的最大值是( )
 如图所示,扇形OPQ的半径为2,圆心角为$\frac{π}{3}$,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,则SABCD的最大值是( )
如图所示,扇形OPQ的半径为2,圆心角为$\frac{π}{3}$,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,则SABCD的最大值是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{2}{3}$ |