题目内容
4.在△ABC中,顶点A的坐标为(3,1),边BC中点D的坐标为(-3,1),则△ABC重心坐标为(-1,1).分析 根据三角形的重心公式与性质,得出向量$\overrightarrow{AD}$=3$\overrightarrow{MD}$,利用坐标表示,即可求出重心坐标.
解答 解:△ABC中,A(3,1),BC的中点为D(-3,1),
设重心M的坐标为(x,y),
则$\overrightarrow{AD}$=3$\overrightarrow{MD}$,
即(-3-3,1-1)=3(-3-x,1-y),
∴$\left\{\begin{array}{l}{-6=3(-3-x)}\\{0=3(1-y)}\end{array}\right.$),
解得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$;
∴△ABC的重心M的坐标为(-1,1).
故答案为:(-1,1).
点评 本题考查了平面向量的坐标运算问题,也考查了三角形的重心公式与性质的应用问题,是基础题目.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13.不等式ax2+4x+a<1+x2对一切x∈R恒成立,则实数a的取值范围是( )
| A. | (3,+∞) | B. | (-∞,-1) | C. | (-∞,1) | D. | (-∞,-1)∪(3,+∞) |
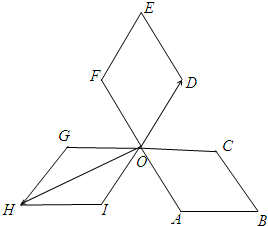 如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )
如图,四边形OABC,ODEF,OGHI是三个全等的菱形,∠COD=∠FOG=∠AOI=60°,P为各菱形边上的动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OH}$,则x+y的最大值为( )