题目内容
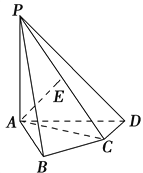
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD= ![]() BC,
BC, ![]() =
= ![]()
![]() .
. 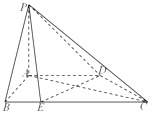
(1)求证:DE⊥平面PAC;
(2)若直线PE与平面PAC所成角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.
【答案】
(1)证明:以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
设AB=AD= ![]() BC=2,
BC=2,
则D(0,2,0),E(2,1,0),A(0,0,0),C(2,4,0),
![]() =(2,﹣1,0),
=(2,﹣1,0), ![]() =(2,4,0),
=(2,4,0),
![]() =4﹣4+0=0,∴DE⊥AC,
=4﹣4+0=0,∴DE⊥AC,
∵PA⊥平面ABCD,DE平面ABCD,∴DE⊥PA,
∵PA∩AC=A,∴DE⊥平面PAC
(2)解:设P(0,0,t),(t>0), ![]() =(0,0,t),
=(0,0,t), ![]() =(2,4,0),
=(2,4,0), ![]() =(2,1,﹣t),
=(2,1,﹣t),
设平面PAC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 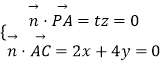 ,取x=2,得
,取x=2,得 ![]() =(2,﹣1,0),
=(2,﹣1,0),
∵直线PE与平面PAC所成角的正弦值为 ![]() ,
,
∴ 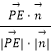 =
= ![]() =
= ![]() ,解得t=1,或t=﹣1(舍),
,解得t=1,或t=﹣1(舍),
∴P(0,0,1), ![]() =(2,4,﹣1),
=(2,4,﹣1), ![]() =(0,2,﹣1),
=(0,2,﹣1),
设平面PCD的法向量 ![]() =(a,b,c),
=(a,b,c),
则 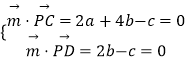 ,取b=1,得
,取b=1,得 ![]() =(﹣1,1,2),
=(﹣1,1,2),
设二面角A﹣PC﹣D的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
二面角A﹣PC﹣D的平面角的余弦值为 ![]() .
.
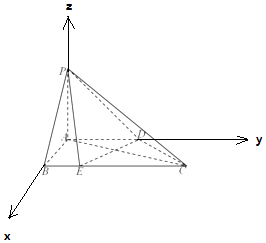
【解析】(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能证明DE⊥平面PAC.(2)求出平面PAC的法向量和平面PCD的法向量,利用向量法能求出二面角A﹣PC﹣D的平面角的余弦值.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想).

 应用题作业本系列答案
应用题作业本系列答案【题目】下表是最近十届奥运会的年份、届别、主办国,以及主办国在上届获得的金牌数、当届
获得的金牌数的统计数据:
年份 | 1972 | 1976 | 1980 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
届别 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
主办国家 | 联邦 德国 | 加拿大 | 苏联 | 美国 | 韩国 | 西班牙 | 美国 | 澳大 利亚 | 希腊 | 中国 |
上届金牌数 | 5 | 0 | 49 | 未参加 | 6 | 1 | 37 | 9 | 4 | 32 |
当界金牌数 | 13 | 0 | 80 | 83 | 12 | 13 | 44 | 16 | 6 | 51 |
某体育爱好组织,利用上表研究所获金牌数与主办奥运会之间的关系,
(1)求出主办国在上届所获金牌数(设为![]() )与在当届所获金牌数(设为
)与在当届所获金牌数(设为![]() )之间的线性回归方程
)之间的线性回归方程
![]() 其中
其中![]()
(2)在2008年第29届北京奥运会上日本获得9块金牌,则据此线性回归方程估计在2020 年第 32 届东
京奥运会上日本将获得的金牌数为(所有金牌数精确到整数)
【题目】为了探究某市高中理科生在高考志愿中报考“经济类”专业是否与性别有关,现从该市高三理科生中随机抽取50各学生进行调查,得到如下2×2列联表:(单位:人).
报考“经济类” | 不报“经济类” | 合计 | |
男 | 6 | 24 | 30 |
女 | 14 | 6 | 20 |
合计 | 20 | 30 | 50 |
(Ⅰ)据此样本,能否有99%的把握认为理科生报考“经济类”专业与性别有关?
(Ⅱ)若以样本中各事件的频率作为概率估计全市总体考生的报考情况,现从该市的全体考生(人数众多)中随机抽取3人,设3人中报考“经济类”专业的人数为随机变量X,求随机变量X的概率分布及数学期望.
附:参考数据:
P(X2≥k) | 0.05 | 0.010 |
k | 3.841 | 6.635 |
(参考公式:X2= ![]() )
)