题目内容

已知正项数列{an}的前n项的乘积等于Tn=(
1
4
)n2-6n（n∈N*），bn=log2an，则数列{bn}的前n项和Sn中最大值是（　　）
A．S6B．S5C．S4D．S3
由已知当n=1时，a1=T1=(
1
4
)-5=45，当n≥2时，an=
Tn
Tn-1
=(
1
4
)2n-7，n=1时也适合上式，
数列{an}的通项公式为an=(
1
4
)2n-7∴bn=log2an=14-4n，数列{bn}是以10为首项，以-4为公差的等差数列．
Sn=10n+
n(n-1)×(-4)
2
=-2n2+12n=-2[（n-3）2-9]，当n=3时取得最大值．
故选D
练习册系列答案
相关题目
已知等比数列{an}单调递增，a1+a4=9，a2a3=8，bn=log22an．
（Ⅰ）求an；
（Ⅱ）若Tn=
1
b1b2
+
1
b2b3
+…+
1
bnbn+1
＞0.99，求n的最小值．
已知等差数列{an}的首项a1=4，公差d＞0，且a1，a5，a21分别是正数等比数列{bn}的b3，b5，b7项．
（Ⅰ）求数列{an}与{bn}的通项公式；
（Ⅱ）设数列{cn}对任意n*均有
c1
b1
+
c2
b2
+…+
cn
bn
=an+1成立，设{cn}的前n项和为Tn，求Tn．
通项公式为an=
2
n(n+1)
的数列{an}的前n项和为
9
5
，则项数n为（　　）
A．7B．8C．9D．10
设数列{an}的前n项和为Sn，且Sn=2n-1．数列{bn}满足b1=2，bn+1-2bn=8an．
（1）求数列{an}的通项公式；
（2）证明：数列{
bn
2n
}为等差数列，并求{bn}的前n项和Tn．
数列{an}满足an+an+1=
1
2
，a2=1，Sn为前n项和，则S21的值为（　　）
A．4B．4.5C．5D．5.5
已知等比数列{an}中，a1=3，a4=81，当数列{bn}满足bn=log3an，则数列{
1
bnbn+1
}的前2013项和S2013为______．
已知点（1，
1
3
）是函数f（x）=ax（a＞0且a≠1）的图象上一点，等比数列{an}的前n项和为f（n）-c，数列{bn}（bn＞0）的首项为c，且前n项和Sn满足Sn-Sn-1=
Sn
+
Sn-1
（n≥2）
（Ⅰ）求数列{an}和{bn}的通项公式
（Ⅱ）求数列{
1
bnbn+1
}前n项和为Tn．
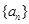已知数列的前n项和为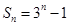，那么该数列的通项公式为=_______.

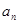违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网