题目内容
已知等比数列{an}单调递增,a1+a4=9,a2a3=8,bn=log22an.
(Ⅰ)求an;
(Ⅱ)若Tn=
+
+…+
>0.99,求n的最小值.
(Ⅰ)求an;
(Ⅱ)若Tn=
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
(I)设等比数列{an}的公比为q,
∵a1+a4=9,a2a3=8,
∴
,解得
或
.
∵等比数列{an}单调递增,∴取
.
∴an=1×2n-1=2n-1.
(II)由(I)可得bn=log2(2×2n-1)=n.
∴
=
=
-
.
∴Tn=1-
,
由Tn>0.99,
∴1-
>1-
,解得n>99.
∴n的最小值是100.
∵a1+a4=9,a2a3=8,
∴
|
|
|
∵等比数列{an}单调递增,∴取
|
∴an=1×2n-1=2n-1.
(II)由(I)可得bn=log2(2×2n-1)=n.
∴
| 1 |
| bnbn+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=1-
| 1 |
| n+1 |
由Tn>0.99,
∴1-
| 1 |
| n+1 |
| 1 |
| 100 |
∴n的最小值是100.

练习册系列答案
相关题目

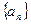 的前
的前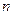 项和
项和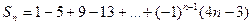 ,
,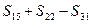 的值。 (2)求
的值。 (2)求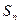 的表达式
的表达式