题目内容
若动圆P恒过定点B(2,0),且和定圆 外切.
外切.
(1)求动圆圆心P的轨迹E的方程;
(2)若过点B的直线l与曲线E交于M、N两点,试判断以MN为直径的圆与直线 是否相交,若相交,求出所截得劣弧的弧度数,若不相交,请说明理由.
是否相交,若相交,求出所截得劣弧的弧度数,若不相交,请说明理由.
 外切.
外切.(1)求动圆圆心P的轨迹E的方程;
(2)若过点B的直线l与曲线E交于M、N两点,试判断以MN为直径的圆与直线
 是否相交,若相交,求出所截得劣弧的弧度数,若不相交,请说明理由.
是否相交,若相交,求出所截得劣弧的弧度数,若不相交,请说明理由.(1)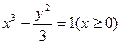 (2)相交
(2)相交 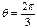
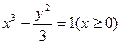 (2)相交
(2)相交 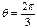
(1)由于圆P与圆C相外切 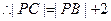 即
即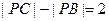
∴动圆P的圆心的轨迹是以B、C为焦点,实轴长为2的双曲线的右支
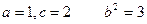
∴动点P的轨迹方程为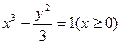 ………………6分(缺少
………………6分(缺少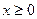 扣1分)
扣1分)
(2)由(1)知B(2,0),直线 为双曲线
为双曲线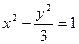 的过右焦点的右准线,则MN为焦点弦.…………………………7分
的过右焦点的右准线,则MN为焦点弦.…………………………7分
当直线l斜率存在时,设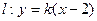 代入
代入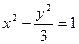 中得:
中得:
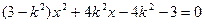
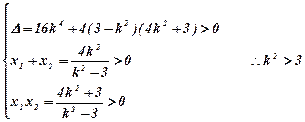
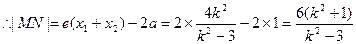
又MN的中点A到直线 的距离
的距离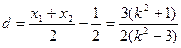
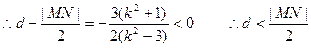
∴以MN为直径的圆与直线 相交.……………………9分
相交.……………………9分
截得劣弧弧度数等于所对圆心角θ的弧度数
又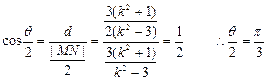
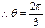
当直线l斜率不存在时,则直线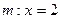 ,经验证上述结论成立.……12分
,经验证上述结论成立.……12分
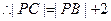 即
即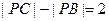
∴动圆P的圆心的轨迹是以B、C为焦点,实轴长为2的双曲线的右支
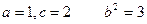
∴动点P的轨迹方程为
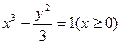 ………………6分(缺少
………………6分(缺少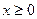 扣1分)
扣1分)(2)由(1)知B(2,0),直线
 为双曲线
为双曲线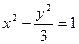 的过右焦点的右准线,则MN为焦点弦.…………………………7分
的过右焦点的右准线,则MN为焦点弦.…………………………7分当直线l斜率存在时,设
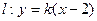 代入
代入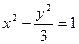 中得:
中得: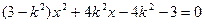
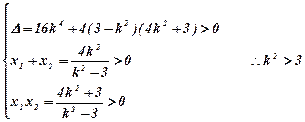
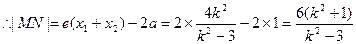
又MN的中点A到直线
 的距离
的距离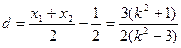
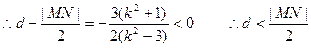
∴以MN为直径的圆与直线
 相交.……………………9分
相交.……………………9分截得劣弧弧度数等于所对圆心角θ的弧度数
又
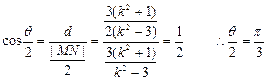
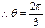
当直线l斜率不存在时,则直线
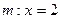 ,经验证上述结论成立.……12分
,经验证上述结论成立.……12分
练习册系列答案
相关题目
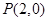 及圆
及圆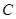 :
: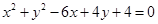 .
.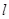 过点
过点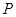 且与圆心
且与圆心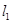 与圆
与圆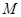 、
、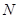 两点,当
两点,当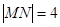 时,求以线段
时,求以线段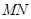 为直径的圆
为直径的圆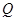 的方程;
的方程;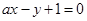 与圆
与圆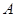 ,
, 两点,是否存在实数
两点,是否存在实数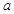 ,使得过点
,使得过点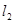 垂直平分
垂直平分 弦
弦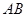 ?若存在,求出实数
?若存在,求出实数 和圆
和圆 关于直线
关于直线 对称,则直线
对称,则直线



 ,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是( )
,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是( ) 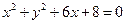 外切,同时与圆
外切,同时与圆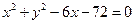 内切,求动圆圆心
内切,求动圆圆心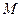 的轨迹方程
的轨迹方程  与
与 的位置关系是( )
的位置关系是( )