题目内容
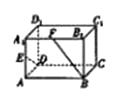
【题目】如图，已知侧棱垂直底面的三棱柱ABC﹣A1B1C1中，AC=3，AB=5，BC=4，点D是AB的中点． 
（1）求证：AC⊥BC；
（2）求证：AC1∥平面CDB1 ．
【答案】
（1）证明：∵AC=3，AB=5，BC=4，
∴AC2+BC2=AB2，
∴AC⊥BC．
（2）证明：以C为原点，CA为x轴，CB为y轴，CC1为z轴，建立空间直角坐标系，
设CC1=t，则由题意得A（3，0，0），C1（0，0，t），C（0，0，0），
B（0，4，0），D（ 
，2，0），B1（0，4，t），
=（ 
）， 
=（0，4，t）， 
=（﹣3，0，t），
设平面CDB1的法向量 
=（x，y，z），
则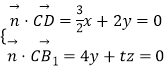 
，取x=2，得 =（4，﹣3， 
），
∴ 
=0，
∵AC1平面CDB1，∴AC1∥平面CDB1．
【解析】（1）利用勾股定理能证明AC⊥BC．（2）以C为原点，CA为x轴，CB为y轴，CC1为z轴，建立空间直角坐标系，利用向量法能证明AC1∥平面CDB1 ．
【考点精析】根据题目的已知条件，利用空间中直线与直线之间的位置关系和直线与平面平行的判定的相关知识可以得到问题的答案，需要掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点；平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．
练习册系列答案
相关题目
