题目内容
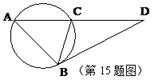
和y轴相切，且和半圆x2+y2=4(0≤x≤2)相内切的动圆圆心P的轨迹方程是
| A．y2=4(x－1)(0＜x≤1) | B．y2=－4(x－1)(0＜x≤1) |
| C．y2=4(x+1)(0＜x≤1) | D．y2=－2(x－1)(0＜x≤1) |
B
设动圆圆心为P(x,y)，由动圆切于y轴，故r=|x|.又由动圆与已知圆内切可知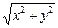
=2－|x|,
整理得y2=－4|x|+4.由于半圆需满足0≤x≤2的条件，∴y2=－4(x－1)(0＜x≤1).
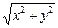=2－|x|,整理得y2=－4|x|+4.由于半圆需满足0≤x≤2的条件，∴y2=－4(x－1)(0＜x≤1).
练习册系列答案
名校课堂系列答案
相关题目
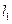
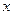
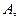
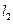
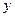
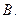
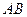将四边形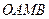
分割成面积相等的两部分，求△AOB的面积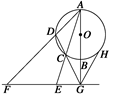
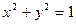为ΔABC的内切园，且BC中点为（1，-1），BC∥x轴。⑴求ΔABC顶点A的轨迹方程。⑵求|BC|的范围。⑶试问ΔABC的面积是否存在最小值？请证明你的判断。
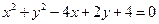关于直线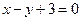
成轴对称的圆的方程是（ ）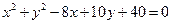
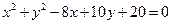
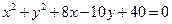
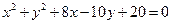
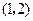且与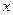
轴相切的圆的方程 ．
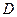作圆的切线切于
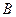点，作割线交圆于
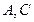两点，其中
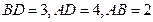，则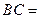
．