题目内容
8.已知⊙O:x2+y2=9,过圆外一点P作⊙O的两条切线,切点分别为A、B.(1)若点P(4,-3),求直线AB的方程;
(2)若点P(x,y)为动点,且∠APB=$\frac{π}{2}$,求点P的轨迹方程.
分析 (1)直线AB可看作已知圆与以OP为直径的圆的交线,求出未知圆的方程,运用两圆方程相减,即可.
(2)设点P的坐标为(x,y),根据∠APB=$\frac{π}{2}$,|PO|=$\sqrt{2}$|OA|=3$\sqrt{2}$,代入整理后即可得到答案.
解答 解:(1)直线AB可看作已知圆与以OP为直径的圆的交线,
以以OP为直径的圆的方程为:(x-2)2+(y+1.5)2=2.25,
将两圆的方程相减得直线AB的方程是4x-3y-9=0;
(2)设点P的坐标为(x,y),则
∵∠APB=$\frac{π}{2}$,
∴|PO|=$\sqrt{2}$|OA|=3$\sqrt{2}$
∴x2+y2=18.
点评 本题考查直线与圆的方程,及位置关系的判断,考查基本的运算能力,属于中档题.

练习册系列答案
相关题目
13.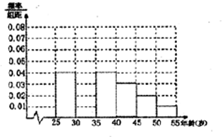 某班同学利用劳动节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
某班同学利用劳动节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
(1)补全频率分布直方图并求n,a,p的值;
(2)请根据(1)中补全的频率分布直方图求抽取n的人的年龄的众数和中位数的估计值.
 某班同学利用劳动节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
某班同学利用劳动节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55) | 15 | 0.3 |
(2)请根据(1)中补全的频率分布直方图求抽取n的人的年龄的众数和中位数的估计值.