题目内容
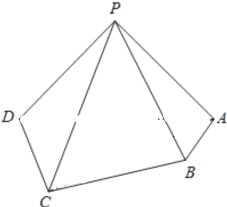
【题目】如图，在几何体
中，四边形
为矩形，
且
，
为
的中点．
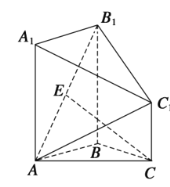
（1）求证：
平面
；
（2）若平面
平面
，
，
，求三棱锥
的体积．
【答案】（1）证明见解析（2）
【解析】
（1）取A1B1中点F，连接EF，FC1， 证明CE∥C1F，即可证明线面平行；
（2）根据三棱锥的等积法得
，即可求得答案.
(1)证明 如图，取A1B1中点F，连接EF，FC1，
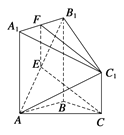
∵E为AB1中点，∴EF//A1A且EF=
A1A，
∵AA1∥CC1且AA1=2CC1，
∴EF//CC1且EF=CC1，即四边形EFC1C为平行四边形，
∴CE∥C1F.
∵
，
，
∴CE∥平面A1B1C1.
(2) ∵平面AB B1A1⊥平面ABC，交线为AB
又矩形AB B1A1中A A1⊥AB，∴AA1⊥平面ABC，
∵AA1∥CC1，∴CC1⊥平面ABC，
∵BB1∥CC1，
，
，
∴BB1∥
，
∴
练习册系列答案
相关题目
