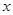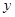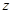题目内容
(本小题满分8分)某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
【答案】
解:设为该儿童分别预订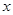 个单位的午餐和
个单位的午餐和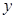 个单位的晚餐,设费用为F,
个单位的晚餐,设费用为F,
 则F
则F ,由题意知:
,由题意知:
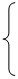
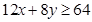
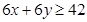
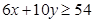
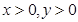 ……………2分
……………2分
画出可行域: ……………2分
变换目标函数: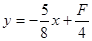 …………2分
…………2分
当目标函数过点A,即直线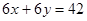 与直线
与直线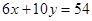 的交点
的交点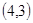 ,
,
F取得最小,即要满足条件,应当为该儿童分别预订4个单位的午餐和3个单位的晚餐。
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(本小题满分8分) 某校在高二年级开设了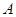 ,
,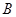 ,
, 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从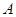 ,
,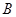 ,
, 三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
|
兴趣小组 |
小组人数 |
抽取人数 |
|
|
24 |
|
|
|
36 |
3 |
|
|
48 |
|
(1)求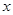 ,
,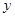 的值;
的值;
(2)若从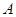 ,
,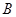 两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组
两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组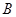 的概率.
的概率.
(本小题满分8分)某高级中学共有学生3000名,各年级男、女生人数如下表:
|
|
高一年级 |
高二年级 |
高三年级 |
|
女生 |
487 |
|
|
|
男生 |
513 |
560 |
|
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是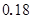 .
.
(1)问高二年级有多少名女生?
(2)现对各年级用分层抽样的方法在全校抽取300名学生,问应在高三年级抽取多少名学生?
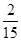 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;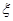 表示获奖的人数,求
表示获奖的人数,求