题目内容
若函数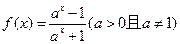 .
.
⑴判断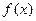 的奇偶性;
的奇偶性;
⑵当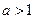 时,判断
时,判断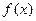 在
在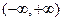 上的单调性,并加以证明
上的单调性,并加以证明
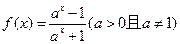 .
.⑴判断
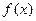 的奇偶性;
的奇偶性;⑵当
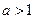 时,判断
时,判断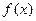 在
在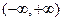 上的单调性,并加以证明
上的单调性,并加以证明(1)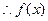 为R上的奇函数(2)当
为R上的奇函数(2)当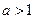 时,
时,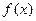 在
在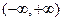 上的单调递增
上的单调递增
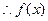 为R上的奇函数(2)当
为R上的奇函数(2)当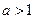 时,
时,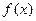 在
在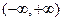 上的单调递增
上的单调递增(1)解:由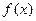 的定义域为
的定义域为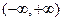 ,关于数0对称……………………2分
,关于数0对称……………………2分
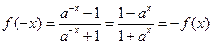 ,得
,得
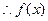 为R上的奇函数.………………………………………………6分
为R上的奇函数.………………………………………………6分
(2)当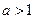 时,
时,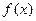 在
在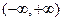 上的单调递增.……8分(本次未扣分,以后考试一定会扣分)
上的单调递增.……8分(本次未扣分,以后考试一定会扣分)
证明:设 为
为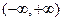 上任意两个实数,且
上任意两个实数,且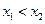 ,则由
,则由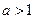 得
得
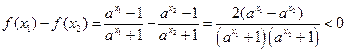
 当
当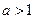 时,
时,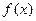 在
在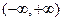 上的单调递增.………………14分
上的单调递增.………………14分
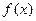 的定义域为
的定义域为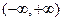 ,关于数0对称……………………2分
,关于数0对称……………………2分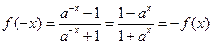 ,得
,得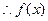 为R上的奇函数.………………………………………………6分
为R上的奇函数.………………………………………………6分(2)当
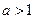 时,
时,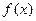 在
在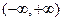 上的单调递增.……8分(本次未扣分,以后考试一定会扣分)
上的单调递增.……8分(本次未扣分,以后考试一定会扣分)证明:设
 为
为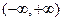 上任意两个实数,且
上任意两个实数,且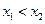 ,则由
,则由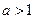 得
得
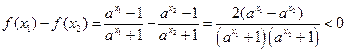
 当
当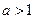 时,
时,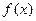 在
在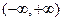 上的单调递增.………………14分
上的单调递增.………………14分
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
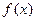 是偶函数,
是偶函数,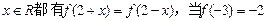 时,
时,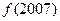 的值为 ( )
的值为 ( )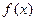 ,对于任意实数x,y都满足
,对于任意实数x,y都满足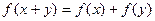 ,且当
,且当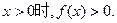 试判断函数的奇偶性与单调性,证明你的结论.
试判断函数的奇偶性与单调性,证明你的结论.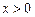 时,
时,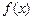 的解析式;
的解析式;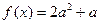 有三个不同的解,求a的取值范围。
有三个不同的解,求a的取值范围。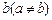 ,当
,当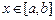 时,
时,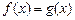 ,且
,且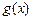 的值域为
的值域为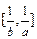 .若存在,求出a、b 的值;若不存在,说明理由
.若存在,求出a、b 的值;若不存在,说明理由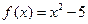 的一个正零点(误差不超过
的一个正零点(误差不超过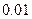 ).
).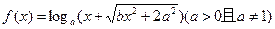 是奇函数,则实数对
是奇函数,则实数对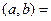 _______
_______ ,
,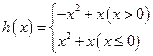 ,
,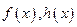 的奇偶性依次为( )
的奇偶性依次为( ) 是偶函数,则a可取值的集合是 ( )
是偶函数,则a可取值的集合是 ( )