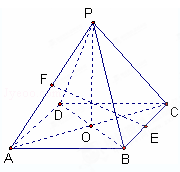
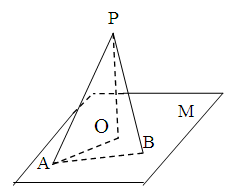
题目内容
如图,直线 平面
平面 ,垂足为
,垂足为 ,直线
,直线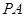 是平面
是平面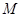 的一条斜线,斜足为
的一条斜线,斜足为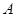 ,其中
,其中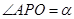 ,过点
,过点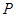 的动直线
的动直线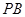 交平面
交平面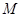 于点
于点 ,
,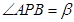 ,则下列说法正确的是___________.
,则下列说法正确的是___________.
①若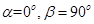 ,则动点B的轨迹是一个圆;
,则动点B的轨迹是一个圆;
②若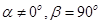 ,则动点B的轨迹是一条直线;
,则动点B的轨迹是一条直线;
③若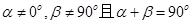 ,则动点B的轨迹是抛物线;
,则动点B的轨迹是抛物线;
④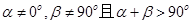 ,则动点B的轨迹是椭圆;
,则动点B的轨迹是椭圆;
⑤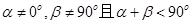 ,则动点B的轨迹是双曲线.
,则动点B的轨迹是双曲线.
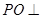 平面
平面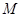 ,垂足为
,垂足为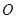 ,直线
,直线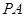 是平面
是平面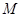 的一条斜线,斜足为
的一条斜线,斜足为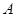 ,其中
,其中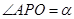 ,过点
,过点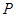 的动直线
的动直线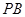 交平面
交平面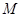 于点
于点 ,
,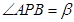 ,则下列说法正确的是___________.
,则下列说法正确的是___________.
①若
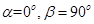 ,则动点B的轨迹是一个圆;
,则动点B的轨迹是一个圆;②若
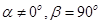 ,则动点B的轨迹是一条直线;
,则动点B的轨迹是一条直线;③若
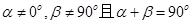 ,则动点B的轨迹是抛物线;
,则动点B的轨迹是抛物线;④
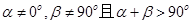 ,则动点B的轨迹是椭圆;
,则动点B的轨迹是椭圆;⑤
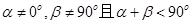 ,则动点B的轨迹是双曲线.
,则动点B的轨迹是双曲线.②③.
试题分析:由①
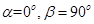 ,
, 与
与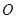 重合,动直线
重合,动直线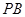 形成一个平面与平面M的平面,动点
形成一个平面与平面M的平面,动点 的轨迹不存在,故不正确;由②
的轨迹不存在,故不正确;由②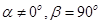 ,则
,则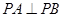 ,所以动直线
,所以动直线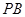 形成一个平面
形成一个平面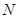 与
与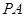 垂直,平面
垂直,平面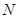 与平面M交于一条直线
与平面M交于一条直线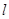 ,则
,则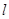 是动点
是动点 的轨迹,故正确;由③
的轨迹,故正确;由③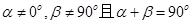 ,则动直线
,则动直线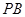 形成一个以
形成一个以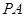 为轴线的圆锥,圆锥母线与轴线的夹角是
为轴线的圆锥,圆锥母线与轴线的夹角是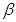 ,由
,由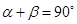 ,则圆锥的一条母线与平面M平行,所以动点
,则圆锥的一条母线与平面M平行,所以动点 的轨迹看成一个平行于圆锥母线的平面截圆锥所成的图形是抛物线,则动点B的轨迹是抛物线,故正确;由④
的轨迹看成一个平行于圆锥母线的平面截圆锥所成的图形是抛物线,则动点B的轨迹是抛物线,故正确;由④ 时,动点
时,动点 的轨迹看成一个与圆锥母线成一个角度的平面截圆锥所成的图形,此时的轨迹是双曲线;由⑤动点
的轨迹看成一个与圆锥母线成一个角度的平面截圆锥所成的图形,此时的轨迹是双曲线;由⑤动点 的轨迹看成一个与圆锥母线成一个角度的平面截圆锥所成的图形,此时的轨迹是椭圆.故最终正确的是②③.
的轨迹看成一个与圆锥母线成一个角度的平面截圆锥所成的图形,此时的轨迹是椭圆.故最终正确的是②③.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
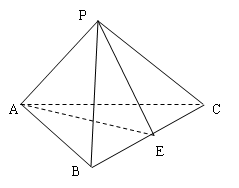
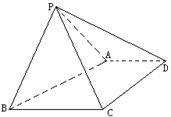
 中,
中,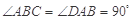 ,
,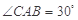 ,
,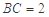 ,
,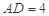 . 把
. 把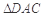 沿对角线
沿对角线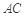 折起到
折起到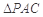 的位置,如图2所示,使得点
的位置,如图2所示,使得点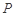 在平面
在平面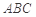 上的正投影
上的正投影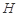 恰好落在线段
恰好落在线段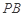 ,点
,点 分别为线段
分别为线段 的中点.
的中点. 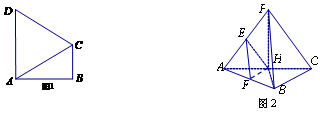
 平面
平面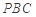 ;
;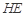 与平面
与平面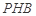 所成角的正弦值;
所成角的正弦值;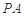 上是否存在一点
上是否存在一点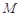 ,使得
,使得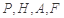 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.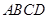 是梯形,
是梯形,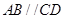 ,
,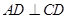 ,三角形
,三角形 是等边三角形,且平面
是等边三角形,且平面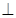 平面
平面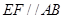 ,
, ,
,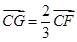
 平面
平面 ;
; 的余弦值.
的余弦值.  中,
中,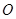 、
、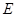 分别是
分别是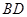 、
、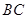 的中点,
的中点,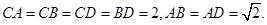
 平面
平面 ;
; 的正切值;
的正切值;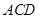 的距离.
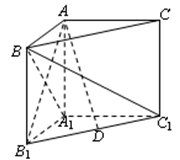
的距离.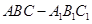 中,
中,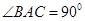 ,
,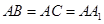 .
.
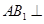 平面
平面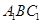 ;
;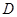 为
为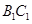 的中点,求
的中点,求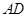 与平面
与平面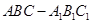 中,
中,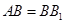 ,
,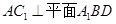 ,
,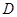 为的
为的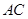 中点.
中点.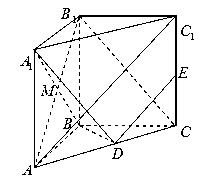
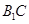 ∥平面
∥平面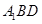 ;
;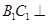 平面
平面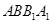 ;
;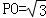 ,E、F分别是BC、AP的中点.
,E、F分别是BC、AP的中点.