题目内容
(如图,在四棱锥P﹣ABCD中,底面是边长为2的菱形,∠BAD=60°,对角线AC与BD相交于点O,PO为四棱锥P﹣ABCD的高,且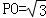 ,E、F分别是BC、AP的中点.
,E、F分别是BC、AP的中点.
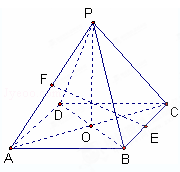
(1)求证:EF∥平面PCD;
(2)求三棱锥F﹣PCD的体积.
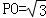 ,E、F分别是BC、AP的中点.
,E、F分别是BC、AP的中点.
(1)求证:EF∥平面PCD;
(2)求三棱锥F﹣PCD的体积.
(Ⅰ)见解析 (Ⅱ)

试题分析:(Ⅰ)取PD边的中点K,不难得到四边形CKFE为平行四边形,从而得到直线EF平行与直线CK,从而得到结论;

(Ⅱ)根据平行关系和三棱锥的体积的轮换对称性,得:
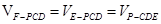 .如本题就是第二种。
.如本题就是第二种。(Ⅱ)中主要是棱锥体积的计算,三棱锥又是一个极其特殊的图形,它的每个顶点均可作为顶点,往往是其解题的技巧之所在,要加以灵活运用.
试题解析:(Ⅰ)取PD的中点K,连接CK,FK,则FK是三角形PAD的中位线,故:
 且
且 ,又因为E为BC的中点,且
,又因为E为BC的中点,且 ,所以
,所以 ,可得四边形CEFK为平行四边形,得
,可得四边形CEFK为平行四边形,得 ,又
,又 ,所以EF∥平面PCD
,所以EF∥平面PCD(Ⅱ)因为EF∥平面PCD,所以点E和点F到平面PDC的距离相等,则有
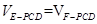 ,故:
,故: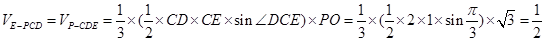

练习册系列答案
相关题目
 的底面是正方形,
的底面是正方形, ,点
,点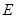 在棱
在棱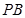 上.
上.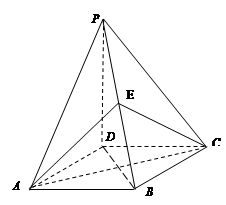
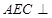 平面
平面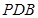 ;
;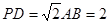 ,且
,且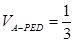 时,确定点
时,确定点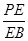 的值.
的值.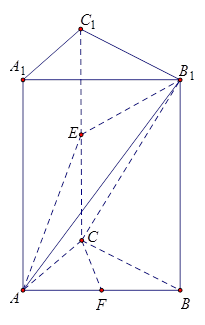
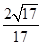 ,若存在,求CE的长,若不存在,请说明理由.
,若存在,求CE的长,若不存在,请说明理由.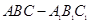 中,
中,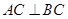 ,点D是AB的中点,
,点D是AB的中点,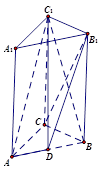
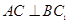 ; (2)
; (2)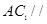 平面
平面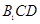
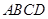 中,
中,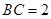 ,
,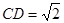 ,
,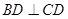 ,正方形
,正方形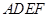 所在平面与平面
所在平面与平面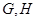 分别是
分别是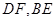 的中点。
的中点。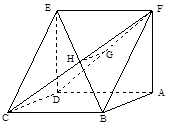
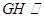 平面
平面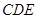 ;
;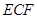 与平面
与平面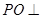 平面
平面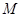 ,垂足为
,垂足为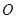 ,直线
,直线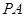 是平面
是平面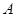 ,其中
,其中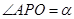 ,过点
,过点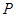 的动直线
的动直线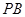 交平面
交平面 ,
,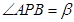 ,则下列说法正确的是___________.
,则下列说法正确的是___________.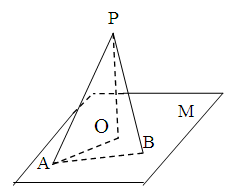
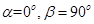 ,则动点B的轨迹是一个圆;
,则动点B的轨迹是一个圆;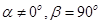 ,则动点B的轨迹是一条直线;
,则动点B的轨迹是一条直线;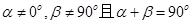 ,则动点B的轨迹是抛物线;
,则动点B的轨迹是抛物线;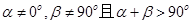 ,则动点B的轨迹是椭圆;
,则动点B的轨迹是椭圆;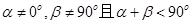 ,则动点B的轨迹是双曲线.
,则动点B的轨迹是双曲线.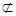 α,则n∥α;
α,则n∥α;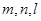 和两个不重合的平面α、β,下列命题中正确命题个数为( )
和两个不重合的平面α、β,下列命题中正确命题个数为( )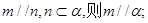
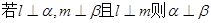
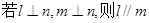
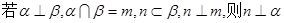
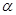 、
、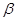 和直线
和直线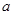 、
、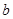 ,若
,若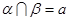 ,
,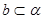 且
且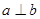 ,则
,则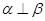 .
.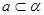 ,
,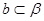 且
且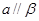 ,
,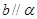 ,则
,则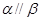 .
.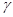 和直线
和直线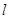 ,若
,若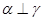 ,
,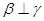 且
且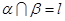 ,则
,则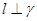 .
.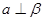 ,则
,则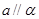 .
.