题目内容
【题目】已知函数f(x)=|x2﹣4|+a|x﹣2|,x∈[﹣3,3].若f(x)的最大值是0,则实数a的取值范围是 .
【答案】(﹣∞,﹣5]
【解析】解:f(x)=|x2﹣4|+a|x﹣2|=|x﹣2|(|x+2|+a)≤0,
当x=2时,f(x)=0恒成立,
当x≠2时,
∴|x+2|+a≤0,
∴a≤﹣|x+2|,
设y=﹣|x+2|,x∈[﹣3,3].则其图象为: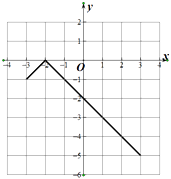
由图象可知ymin=﹣5,
a≤﹣5,
故实数a的取值范围是(﹣∞,﹣5],
所以答案是:(﹣∞,﹣5]
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.

练习册系列答案
相关题目