题目内容
在平面斜坐标系xOy中∠xOy=45°,点P的斜坐标定义为:若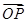 =x0e1+y0e2(其中e1,e2分别为与斜坐标系的x轴,y轴同方向的单位向量),则点P的坐标为(x0,y0).若F1(-1,0),F2(1,0),且动点M(x,y)满足|
=x0e1+y0e2(其中e1,e2分别为与斜坐标系的x轴,y轴同方向的单位向量),则点P的坐标为(x0,y0).若F1(-1,0),F2(1,0),且动点M(x,y)满足| 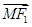 |=|
|=|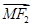 |,则点M在斜坐标系中的轨迹方程为( )
|,则点M在斜坐标系中的轨迹方程为( )
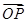 =x0e1+y0e2(其中e1,e2分别为与斜坐标系的x轴,y轴同方向的单位向量),则点P的坐标为(x0,y0).若F1(-1,0),F2(1,0),且动点M(x,y)满足|
=x0e1+y0e2(其中e1,e2分别为与斜坐标系的x轴,y轴同方向的单位向量),则点P的坐标为(x0,y0).若F1(-1,0),F2(1,0),且动点M(x,y)满足| 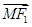 |=|
|=|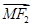 |,则点M在斜坐标系中的轨迹方程为( )
|,则点M在斜坐标系中的轨迹方程为( )A.x-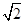 y=0 y=0 | B.x+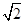 y=0 y=0 | C.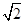 x-y=0 x-y=0 | D.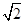 x+y=0 x+y=0 |
D
根据已知|e1|=|e2|=1,〈e1,e2〉=45°,故e1·e2=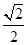 ,
,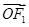 =-e1,
=-e1,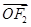 =e1.设
=e1.设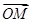 =xe1+ye2,由|
=xe1+ye2,由|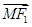 |=|
|=|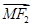 |,可得|
|,可得|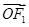 -
-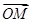 |=|
|=|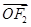 -
-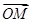 |,即|-(1+x)e1-ye2|=|(1-x)e1-ye2|,两端平方得(1+x)2+2(1+x)y×
|,即|-(1+x)e1-ye2|=|(1-x)e1-ye2|,两端平方得(1+x)2+2(1+x)y×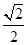 +y2=(1-x)2-2(1-x)y×
+y2=(1-x)2-2(1-x)y×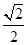 +y2,化简整理得
+y2,化简整理得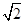 x+y=0.
x+y=0.
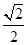 ,
,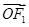 =-e1,
=-e1,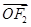 =e1.设
=e1.设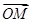 =xe1+ye2,由|
=xe1+ye2,由|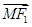 |=|
|=|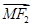 |,可得|
|,可得|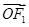 -
-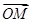 |=|
|=|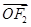 -
-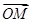 |,即|-(1+x)e1-ye2|=|(1-x)e1-ye2|,两端平方得(1+x)2+2(1+x)y×
|,即|-(1+x)e1-ye2|=|(1-x)e1-ye2|,两端平方得(1+x)2+2(1+x)y×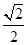 +y2=(1-x)2-2(1-x)y×
+y2=(1-x)2-2(1-x)y×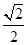 +y2,化简整理得
+y2,化简整理得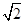 x+y=0.
x+y=0.
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
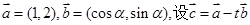 (
(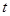 为实数).
为实数).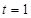 时,若
时,若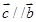 ,求
,求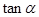 ;
;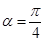 ,求
,求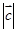 的最小值,并求出此时向量
的最小值,并求出此时向量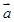 在
在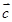 方向上的投影.
方向上的投影.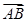 =
=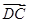 ,则A、B、C、D四点构成平行四边形;
,则A、B、C、D四点构成平行四边形;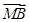 -
-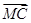 )·(
)·(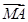 )=0,则△ABC为________三角形.
)=0,则△ABC为________三角形.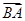 ·
·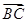 -
-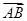 2=0,则△ABC的面积为________.
2=0,则△ABC的面积为________.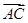 =(1,2),
=(1,2),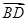 =(-4,2),则该四边形的面积为( )
=(-4,2),则该四边形的面积为( )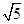
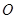 为
为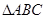 内一点,若对任意
内一点,若对任意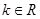 ,恒有
,恒有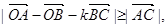 则
则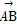 =a+4b,
=a+4b,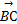 =-a+9b,
=-a+9b,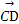 =3a-b,则一定共线的是( )
=3a-b,则一定共线的是( )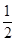 AB,BE=
AB,BE=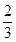 BC.若
BC.若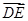 =λ1
=λ1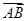 +λ2
+λ2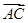 (λ1,λ2为实数),则λ1+λ2的值为________.
(λ1,λ2为实数),则λ1+λ2的值为________.