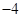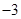题目内容
为保增长、促发展,某地计划投资甲、乙两个项目,根据市场调研,知甲项目每投资100万元需要配套电能2万千瓦时,可提供就业岗位24个,GDP增长260万元;乙项目每投资100万元需要配套电能4万千瓦时,可提供就业岗位36个,GDP增长200万元.已知该地为甲、乙两个项目最多可投资3000万元,配套电能100万千瓦时,若要求两个项目能提供的就业岗位不少于840个,问如何安排甲、乙两个项目的投资额,才能使GDP增长的最多.
当甲项目投资2000万元,乙项目投资1000万元时,GDP增长得最多.
解:设甲项目投资x万元,乙项目投资y万元,增长的GDP为z万元,则投资甲、乙两个项目可增长的GDP为z=2.6x+2y.
依题意,知x、y满足
则此不等式组所表示的平面区域如图中阴影部分所示.

把z=2.6x+2y变形为y=-1.3x+0.5z,其在y轴上的截距为0.5z.
由图可知当直线y=-1.3x+0.5z经过可行域上的点B时,其纵截距取得最大值,也即z取得最大值.
由
得x=2000,y=1000,
即点B的坐标为(2000,1000),
故当甲项目投资2000万元,乙项目投资1000万元时,GDP增长得最多.
依题意,知x、y满足

则此不等式组所表示的平面区域如图中阴影部分所示.

把z=2.6x+2y变形为y=-1.3x+0.5z,其在y轴上的截距为0.5z.
由图可知当直线y=-1.3x+0.5z经过可行域上的点B时,其纵截距取得最大值,也即z取得最大值.
由

得x=2000,y=1000,
即点B的坐标为(2000,1000),
故当甲项目投资2000万元,乙项目投资1000万元时,GDP增长得最多.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 满足
满足 ,则
,则 的最大值是 .
的最大值是 . ,则
,则 的最大值是( )
的最大值是( )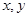 满足约束条件
满足约束条件 则目标函数
则目标函数 的最小值为( )
的最小值为( ) 满足约束条件
满足约束条件 ,且
,且 的最小值为
的最小值为 ,则
,则
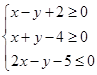 ,若目标函数z=y-ax取得最大值时的唯一最优解是(1,3),求实数a的取值范围.
,若目标函数z=y-ax取得最大值时的唯一最优解是(1,3),求实数a的取值范围.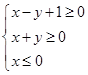 则z=3x+2y的最小值是( )
则z=3x+2y的最小值是( )
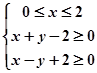 ,则其表示的平面区域的面积是( )
,则其表示的平面区域的面积是( )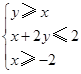 ,则z=x-3y的最大值为( )
,则z=x-3y的最大值为( )