题目内容

已知椭圆E的离心率为e，两焦点为F1、F2，抛物线C以F1为顶点，F2为焦点，P为两曲线的一个交点，若
|PF1|
|PF2|
=e，则e的值为______．
作PT垂直椭圆准线l于T
则由椭圆第二定义
|PF1|：|PT|=e
又|PF1|：|PF2|=e
故|PT|=|PF2|
由抛物线定义知l为抛物线准线
故F1到l的距离等于F1到F2的距离，
即（-c）-（-
a2
c
）=c-（-c）
得e=
c
a
=
3
3
．
故答案为：
3
3
．
练习册系列答案
相关题目
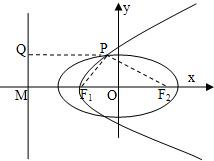精英家教网已知椭圆E的离心率为e，两焦点为F1，F2，抛物线C以F1为顶点，F2为焦点，P为两曲线的一个公共点，若
|PF1|
|PF2|
=e，则e的值为（　　）
A、
3
3
B、
3
2
C、
2
2
D、
6
3
已知椭圆E的离心率为e，两焦点为F1、F2，抛物线C以F1为顶点，F2为焦点，P为两曲线的一个交点，若
|PF1|
|PF2|
=e，则e的值为
3
3
3
3
．
（A题） （奥赛班做）已知椭圆E的离心率为e，左右焦点分别为F1、F2，抛物线C以F1顶点，F2为焦点，P为两曲线的一个交点，
|PF1|
|PF2|
=e，则e的值为
3
3
3
3
．
已知椭圆E的离心率为e，两焦点为F1，F2，抛物线C以F1为顶点，F2为焦点，P为两曲线的一个交点，若=e，则e的值为_________.

已知椭圆E的离心率为e,两焦点为F1、F2，抛物线C以F1为顶点，F2为焦点，P为两曲线的一个交点，若=e，则e的值为(    )

A.                    B.              C.                D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网