题目内容
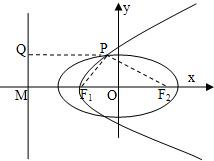 已知椭圆E的离心率为e,两焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个公共点,若
已知椭圆E的离心率为e,两焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个公共点,若| |PF1| |
| |PF2| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:抛物线的准线l交x轴于M,P在l上的射影为Q,进而可推断出|F1M|=|F1F2|,则l的方程可知推知|PF2|=|PQ|,,利用
=e推断出
=e进而根据椭圆的第二定义可知l为椭圆的左准线,进而推断出-3c=-
求得椭圆的离心率.
| |PF1| |
| |PF2| |
| |PF1| |
| |PQ| |
| a2 |
| c |
解答:解:记抛物线的准线l交x轴于M,P在l上的射影为Q,则|F1M|=|F1F2|=2c,
即l的方程为x=-3c,|PF2|=|PQ|,又
=e,即
=e,
∵F1是椭圆的左焦点,
∴|PQ|为P到椭圆左准线的距离,即l为椭圆的左准线,
于是有:-3c=-
?e=
,
故选A
即l的方程为x=-3c,|PF2|=|PQ|,又
| |PF1| |
| |PF2| |
| |PF1| |
| |PQ| |
∵F1是椭圆的左焦点,
∴|PQ|为P到椭圆左准线的距离,即l为椭圆的左准线,
于是有:-3c=-
| a2 |
| c |
| ||
| 3 |
故选A
点评:本题主要考查了抛物线的简单性质,椭圆的简单性质.抛物线的定义等.考查了学生对圆锥曲线基础知识掌握的熟练程度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目