题目内容
【题目】已知一次函数
是
上的减函数，
,且 f [ f(x)]=16x-3.
（1）求；
（2）若
在(-2,3)单调递增，求实数
的取值范围；
（3）当
时，有最大值1，求实数的值.
【答案】（1）
； （2）
； （3）
.
【解析】
⑴设
，结合题意运用待定系数法求出表达式
⑵表示出
的解析式，结合单调性求出
的取值范围
⑶讨论对称轴与区间的位置关系，求出实数的值
（1）∵
是
上的增函数，
设f(x)=ax+b(a<0)
故f[f(x)]=a(ax+b)+b=a2x+ab+b=16x-3,
∴a=16,ab+b=-5,解得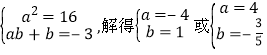
由于a<0,得a=-4,b=1 ,∴f(x)=-4x+1.
（2）
=(-4x+1)(x+m)=-4x2+(1-4m)x+m
对称轴
，根据题意可得
3， 解得
,
∴的取值范围为
。
（3）①当 
即
时,
，解得m=
，符合题意；
②当>1时，即
时,
=1,解得m=
,
不符合题意；
由①②可得m=.
练习册系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打篮球时间x单位：小时）与当天投篮命中率y之间的关系：
时间x | 1 | 2 | 3 | 4 | 5 |
命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
（1）求小李这5天的平均投篮命中率；
（2）用线性回归分析的方法，预测小李该月6号打6小时篮球的投篮命中率． 
．
