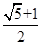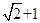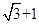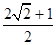题目内容
如图,抛物线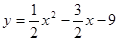 与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
与x轴交于A、B两点,与y轴交于点C,连接BC、AC。

(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合)。过点E作直线l平行BC,交AC于点D。设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留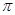 )。
)。
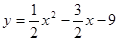 与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合)。过点E作直线l平行BC,交AC于点D。设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留
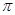 )。
)。(1)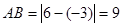 ,
,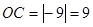 ,(2)
,(2)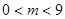 (3)
(3)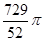
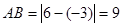 ,
,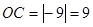 ,(2)
,(2)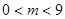 (3)
(3)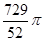
试题分析:解:(1)令y=0,即
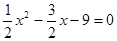 ,
,整理得
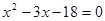 ,
,解得:
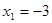 ,
,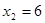 ,
,∴ A(—3,0),B(6,0)
令x = 0,得y = —9,
∴ 点C(0,—9)
∴
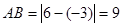 ,
,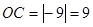 , 3分
, 3分(2)
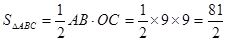 ,
,∵ l∥BC,
∴ △ADE∽△ACB,
∴
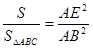 ,即
,即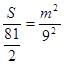
∴
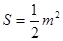 ,其中
,其中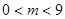 。 6分
。 6分(3)
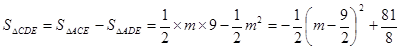 ,
,∵
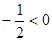
∴ 当
 时,S△CDE取得最大值,且最大值是
时,S△CDE取得最大值,且最大值是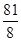 。
。这时点E(
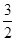 ,0),
,0),∴
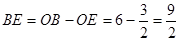 ,
,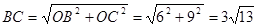 ,
,作EF⊥BC,垂足为F,
∵∠EBF=∠CBO,∠EFB=∠COB,
∴△EFB∽△COB,
∴
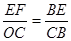 ,即
,即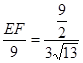
∴
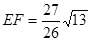 ,
,∴ ⊙E的面积为:
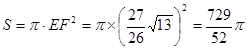 。
。答:以点E为圆心,与BC相切的圆的面积为
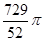 。 11分
。 11分点评:该题主要考查了二次函数的性质、相似三角形的性质、图形面积的求法等综合知识.在解题时,要多留意图形之间的关系,有些时候将所求问题进行时候转化可以大大的降低解题的难度.

练习册系列答案
相关题目
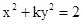 表示焦点在y轴的椭圆,那么实数k的取值范围是____________。
表示焦点在y轴的椭圆,那么实数k的取值范围是____________。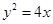 的焦点作一条倾斜角为
的焦点作一条倾斜角为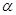 ,长度不超过8的弦,弦所在的直线与圆
,长度不超过8的弦,弦所在的直线与圆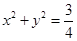
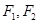 是椭圆
是椭圆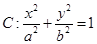
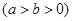 的左、右焦点,点
的左、右焦点,点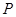 在椭圆
在椭圆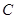 上,线段
上,线段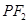 与圆
与圆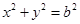 相切于点
相切于点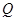 ,且点
,且点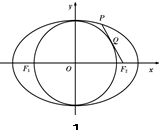
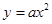 的准线方程为
的准线方程为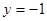 ,则实数
,则实数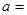 ( )
( )
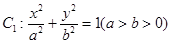 的右焦点
的右焦点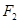 与抛物线
与抛物线 的焦点重合,左端点为
的焦点重合,左端点为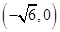
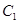 的右焦点且斜率为
的右焦点且斜率为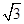 的直线
的直线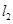 被椭圆
被椭圆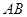 。
。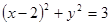 ,此圆与抛物线
,此圆与抛物线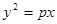
 有四个不同的交点,若在
有四个不同的交点,若在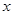 轴上方的两交点分别为
轴上方的两交点分别为 ,
,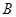 ,坐标原点为
,坐标原点为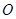 ,
,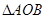 的面积为
的面积为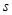 。
。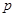 的取值范围;
的取值范围;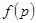 的表达式及
的表达式及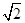
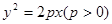 与双曲线
与双曲线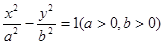 有相同的焦点
有相同的焦点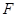 ,点
,点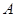 是两曲线的交点,且
是两曲线的交点,且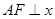 轴,则双曲线的离心率为( )
轴,则双曲线的离心率为( )