题目内容
定义在R上的函数f (x)满足:如果对任意x1,x2![]() R,都有
R,都有![]() ,则称函数f (x)是R上的凹函数.已知二次函数
,则称函数f (x)是R上的凹函数.已知二次函数![]() .w.w.w.k.s.5.u.c.o.m
.w.w.w.k.s.5.u.c.o.m ![]()
(1)当![]() 时,试判断函数f (x)是否为凹函数,并说明理由;
时,试判断函数f (x)是否为凹函数,并说明理由;
(2)如果函数f (x)对任意的x![]() [0,1]时,都有
[0,1]时,都有![]() ,试求实数a的范围。
,试求实数a的范围。
解析:(1)a=1时,函数f (x)是凹函数。
此时 ![]() ,
,
![]() = (
= (![]() )2 + (
)2 + (![]() ),
),
![]() [f (x1) + f (x2)] =
[f (x1) + f (x2)] =![]() [x
[x![]() + x1 + x
+ x1 + x![]() + x2],
+ x2],
作差得到: ![]() 2
2 ![]() [f (x1) + f (x2)]
[f (x1) + f (x2)]
= (![]() )2 + (
)2 + (![]() )
) ![]() (x
(x![]() + x
+ x![]() )
) ![]() (x1 + x2) w.w.w.k.s.5.u.c.o.m
(x1 + x2) w.w.w.k.s.5.u.c.o.m ![]()
= ![]()
= ![]() =
=![]() 0,
0,
即有![]()
![]() [f (x1) + f (x2)],
[f (x1) + f (x2)],
故知函数![]() 为凹函数 w.w.w.k.s.5.u.c.o.m
为凹函数 w.w.w.k.s.5.u.c.o.m ![]()
(2)由![]()
则有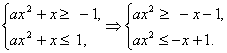
i)若x = 0时,则a![]() R恒成立.
R恒成立.
ii)若x![]()
![]() 时,有
时,有
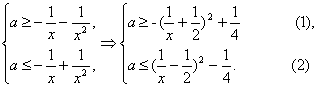
![]()
![]()
![]() .w.w.w.k.s.5.u.c.o.m
.w.w.w.k.s.5.u.c.o.m ![]()
∴当![]() = 1时,[ (
= 1时,[ (![]() +
+![]() )2 +
)2 +![]() ]max = 2,所以
]max = 2,所以![]() ,
,
[ (![]()
![]() )2
)2 ![]() ]min = 0,所以
]min = 0,所以![]() .
.

练习册系列答案
相关题目