题目内容
在锐角 内角
内角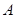 、
、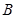 、
、 所对的边分别为
所对的边分别为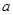 、
、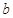 、
、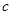 .已知
.已知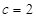 ,
,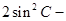
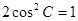 .
.
求:(1) 外接圆半径;
外接圆半径;
(2)当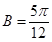 时,求
时,求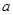 的大小.
的大小.
(1) 外接圆的半径为
外接圆的半径为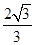 ;(2)
;(2)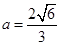 .
.
解析试题分析:(1)先利用同角三角函数的平方关系算出 的值,并结合角
的值,并结合角 的范围求出角
的范围求出角 的值,最后利用正弦定理求出
的值,最后利用正弦定理求出 的外接圆半径;(2)由角
的外接圆半径;(2)由角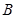 、
、 的值结合三角形的内角和定理求出角
的值结合三角形的内角和定理求出角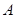 ,然后利用正弦定理求出
,然后利用正弦定理求出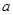 的值.
的值.
试题解析:(1)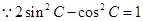 ,即
,即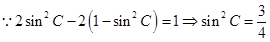 ,
,
因为 为锐角,则
为锐角,则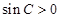 ,所以
,所以 ,
,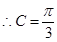 ,
,
设 的外接圆半径为
的外接圆半径为 ,由正弦定理得
,由正弦定理得 ,解得
,解得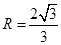 ,
,
故 外接圆的半径为
外接圆的半径为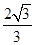 ;
;
(2)当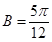 ,
,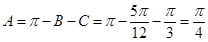 ,
,
由正弦定理得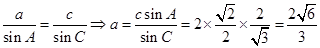 .
.
考点:1.正弦定理;2.三角形的内角和定理

练习册系列答案
相关题目
 中,角
中,角 所对的边分别为
所对的边分别为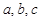 ,且
,且 ,
, ,求
,求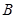 的取值范围.
的取值范围. 中,角
中,角 所对的边分别为
所对的边分别为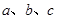 ,已知
,已知 ,
, 的大小;
的大小;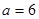 ,求
,求 的取值范围.
的取值范围. 的顶点
的顶点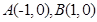 ,顶点
,顶点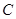 在直线
在直线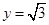 上;
上;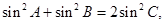 求点
求点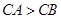 ,且
,且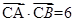 ,求角
,求角 ,已知石塔的高度为
,已知石塔的高度为 .
.
 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点
处测得地面上一点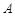 的俯角为
的俯角为 ,在塔底
,在塔底 处测得
处测得 ,用
,用 表示山的高度
表示山的高度 ;
; 上,其中
上,其中 是塔顶
是塔顶 ,当观测点
,当观测点 在
在 时看
时看 )最大,求山的高度
)最大,求山的高度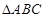 中,角
中,角 所对的边分别为
所对的边分别为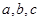 ,已知
,已知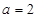 ,
,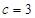 ,
,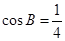 .
.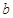 的值;
的值;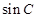 的值.
的值.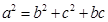 .
.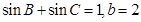 ,试求△ABC的面积.
,试求△ABC的面积.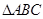 中,角
中,角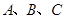 的对边分别为
的对边分别为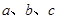 ,且有
,且有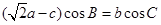 .
.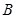 的大小;
的大小;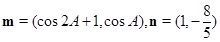 ,且
,且 ,求
,求 的值.
的值. 中,设
中,设 、
、 、
、 分别为角
分别为角 、
、 、
、 的对边,角
的对边,角 交
交 边于
边于 ,
,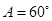 .
. ;
; ,
, ,求其三边
,求其三边