题目内容
如图,A是△BCD所在平面外一点,∠ABD=∠ACD=90°,AB=AC,E是BC的中点.求证:(1)AD⊥BC;
(2)△AED是钝角三角形.
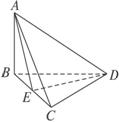
证明:(1)∵AB=AC,E是BC的中点,∴BC⊥AE.
在△ABD、△ACD中,∠ABD=∠ACD=90°,AB=AC,AD=AD,∴△ABD≌△ACD.∴BD=DC.
又E是BC的中点,∴BC⊥ED.又BC⊥AE,AE∩ED=E,∴BC⊥平面AED.又AD![]() 平面AED,∴AD⊥BC.
平面AED,∴AD⊥BC.
(2)∵AE2=AB2-![]() BC2,ED2=DC2-
BC2,ED2=DC2-![]() BC2=BD2-
BC2=BD2-![]() BC2,AD2=AB2+BD2,
BC2,AD2=AB2+BD2,
∴cos∠AED=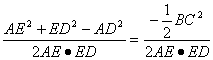 <0.
<0.
∴∠AED为钝角.故△AED为钝角三角形.

练习册系列答案
相关题目
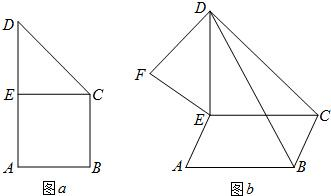 如图a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=
如图a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=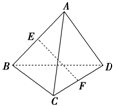 如图,点A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点.
如图,点A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点.

