题目内容
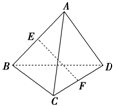 如图,点A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点.
如图,点A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点.(1)若EF=
| ||
| 2 |
(2)若EF=
| ||
| 2 |
分析:设G是AC的中点,连结EG、FG,则EG与FG所成的锐角(或直角)为AD与BC所成的角,利用余弦定理,结合异面直线所成角的范围,即可得到结论.
解答: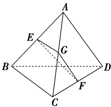 解:设G是AC的中点,连结EG、FG.如图所示.
解:设G是AC的中点,连结EG、FG.如图所示.
∵E、F分别是AB、CD的中点,
∴EG∥BC且EG=
BC,FG∥AD且FG=
AD.
∵AD=BC,
∴EG=FG=
AD,
∴EG与FG所成的锐角(或直角)为AD与BC所成的角.
(1)若EF=
AD,则在△EFG中有cos∠EGF=
=
=0,
∴∠EGF=90°,即AD与BC所成的角为90°.
(2)若EF=
AD,则在△EFG中有cos∠EGF=
=
=-
,
∴∠EGF=120°,其补角为60°,
即AD与BC所成的角为60°.
 解:设G是AC的中点,连结EG、FG.如图所示.
解:设G是AC的中点,连结EG、FG.如图所示.∵E、F分别是AB、CD的中点,
∴EG∥BC且EG=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=BC,
∴EG=FG=
| 1 |
| 2 |
∴EG与FG所成的锐角(或直角)为AD与BC所成的角.
(1)若EF=
| ||
| 2 |
| EG2+FG2-EF2 |
| 2EG•FG |
=
(
| ||||||||
2•(
|
∴∠EGF=90°,即AD与BC所成的角为90°.
(2)若EF=
| ||
| 2 |
| EG2+FG2-EF2 |
| 2EG•FG |
=
(
| ||||||||
2•(
|
| 1 |
| 2 |
∴∠EGF=120°,其补角为60°,
即AD与BC所成的角为60°.
点评:本题考查异面直线所成角,考查余弦定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
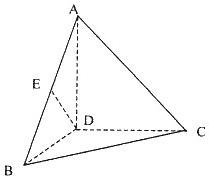 如图,四面体A-BCD中,AD⊥BD,AD⊥CD,BD⊥CD,且AD=BD=CD=2,点E是线段AB的中点.
如图,四面体A-BCD中,AD⊥BD,AD⊥CD,BD⊥CD,且AD=BD=CD=2,点E是线段AB的中点. (2013•文昌模拟)如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设
(2013•文昌模拟)如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设 如图三棱锥A-BCD中,截面四边形EFGH是梯形,其中EF∥GH,点E,F,G,H分别在AB、BC、CD、DA上;
如图三棱锥A-BCD中,截面四边形EFGH是梯形,其中EF∥GH,点E,F,G,H分别在AB、BC、CD、DA上;