题目内容
点A是BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点,且EF=![]() AD,求异面直线AD和BC所成的角。(如图)
AD,求异面直线AD和BC所成的角。(如图)

解析:
设G是AC中点,连接DG、FG。因D、F分别是AB、CD中点,故EG∥BC且EG=![]() BC,FG∥AD,且FG=
BC,FG∥AD,且FG=![]() AD,由异面直线所成角定义可知EG与FG所成锐角或直角为异面直线AD、BC所成角,即∠EGF为所求。由BC=AD知EG=GF=
AD,由异面直线所成角定义可知EG与FG所成锐角或直角为异面直线AD、BC所成角,即∠EGF为所求。由BC=AD知EG=GF=![]() AD,又EF=AD,由余弦定理可得cos∠EGF=0,即∠EGF=90°。
AD,又EF=AD,由余弦定理可得cos∠EGF=0,即∠EGF=90°。
注:本题的平移点是AC中点G,按定义过G分别作出了两条异面直线的平行线,然后在△EFG中求角。通常在出现线段中点时,常取另一线段中点,以构成中位线,既可用平行关系,又可用线段的倍半关系。

练习册系列答案
相关题目
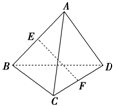 如图,点A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点.
如图,点A是△BCD所在平面外一点,AD=BC,E、F分别是AB、CD的中点.
