题目内容

2．已知实数a，b，c，d满足a+b=c+d≠0，a3+b3=c3+d3，求证：（a-c）（a-d）=0．

分析 由题意可得a2-ab+b2=c2-cd+d2，从而可得ab=cd，（a-b）2=（c-d）2，从而证明可得．

解答 证明：∵a3+b3=c3+d3，
∴（a+b）（a2-ab+b2）=（c+d）（c2-cd+d2），
又∵a+b=c+d≠0，
∴a2-ab+b2=c2-cd+d2，
∴（a+b）2-3ab=（c+d）2-3cd；
∴ab=cd，
又∵（a-b）2+ab=（c-d）2+cd，
∴（a-b）2=（c-d）2，
∴a-b=c-d或a-b=d-c；
若a-b=c-d，与a+b=c+d联立可得，
a=c；
若a-b=d-c，与a+b=c+d联立可得，
a=d；
故（a-c）（a-d）=0．

点评 本题考查了立方和公式的应用及完全平方公式的化简与运用．

练习册系列答案
相关题目
12．若执行如图的程序框图，则输出的s值是（　　）
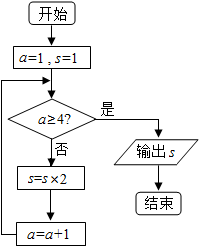
A．2B．4C．6D．8
13．设a是实数，函数f（x）=e2x+|ex-a|（x∈R）．
（1）求证；f（x）不是奇函数；
（2）当a≤0时，解关于x的不等式 f（x）＞a2；
（3）求函数f（x）的值域（用a表示）．
10．如图，在△ABC中，AB+AC=2BC，G为重心，I为内心．证明：GI∥BC．
17．执行如图所示的程序框图（算法流程图），输出的n为（　　）
A．3B．4C．5D．6
7．已知x，y是三角形的两边，α，β是三角形的两内角，且x，y，α，β之间满足下列关系$\left\{\begin{array}{l}{xsinα+ycosβ=0}\\{xcosα-ysinβ=0}\end{array}\right.$，则α的值为（　　）
A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{2π}{3}$
14．等差数列{an}的前n项和为Sn，且4a1，2a2，a3成等比数列．若a1=3，则S4=（　　）
A．7B．8C．12D．16
11．已知函数f（x）的定义域是[-1，2]，则y=f（x）+f（-x）的定义域是（　　）
A．[-1，1]B．[-2，2]C．[-1，2]D．[-2，1]
12．函数f（x）=logax与g（x）=b-x其中a＞0，a≠1，ab=1）的图象可能是（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网