题目内容
10.如图,在△ABC中,AB+AC=2BC,G为重心,I为内心.证明:GI∥BC.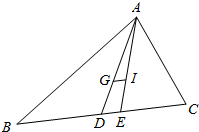
分析 根据已知和三角形内角平分线定理,可得$\frac{AI}{IE}$=2,结合重心的性质,可得$\frac{AI}{IE}$=$\frac{AG}{GD}$,进而得到答案.
解答 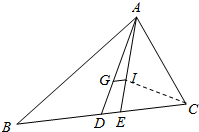 证明:∵I为△ABC内心.
证明:∵I为△ABC内心.
∴AE为∠BAC的角平分线,
∴$\frac{AB}{AC}$=$\frac{BE}{CE}$,
∴$\frac{AB+AC}{AC}$=$\frac{BE+CE}{CE}$,
∴$\frac{2BC}{AC}$=$\frac{BC}{CE}$
∴AC=2CE,
又∵CI为∠C的平分线,
故$\frac{AC}{CE}$=$\frac{AI}{IE}$=2,
又∵G为△ABC重心.
∴$\frac{AG}{GD}$=2,
即$\frac{AI}{IE}$=$\frac{AG}{GD}$,
故GI∥BC
点评 本题考查的知识点是三角形的四心,三角形内角平分线定理,平行线分线段成比例定理,难度中档.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
20.从6名同学中选出2名参加某一项活动,有( )种不同的选法.
| A. | 30 | B. | 36 | C. | 15 | D. | 40 |
1.给出如图的程序框图,那么输出的数是( )


| A. | 2450 | B. | 2550 | C. | 4900 | D. | 5050 |
5.已知某算法的流程图如图所示,则程序运行结束时输出的结果为( )
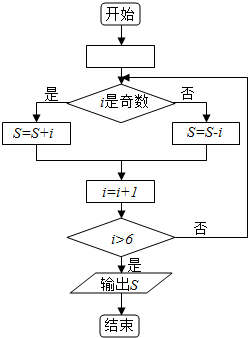

| A. | 5 | B. | 3 | C. | -5 | D. | -3 |
15.执行如图的程序框图,输出的结果为( )
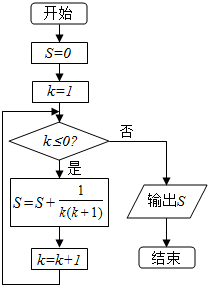

| A. | $\frac{8}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{10}{11}$ | D. | $\frac{9}{8}$ |