题目内容
7.已知x,y是三角形的两边,α,β是三角形的两内角,且x,y,α,β之间满足下列关系$\left\{\begin{array}{l}{xsinα+ycosβ=0}\\{xcosα-ysinβ=0}\end{array}\right.$,则α的值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
分析 利用$\left\{\begin{array}{l}{xsinα+ycosβ=0}\\{xcosα-ysinβ=0}\end{array}\right.$,移向平方相加可得x=y,两式平方相加可得sin(α-β)=-1,可得α-β=-$\frac{π}{2}$,再分类讨论,即可得出结论.
解答 解:∵$\left\{\begin{array}{l}{xsinα+ycosβ=0}\\{xcosα-ysinβ=0}\end{array}\right.$,
∴移向平方相加可得x=y,
两式平方相加可得sin(α-β)=-1
∴α-β=-$\frac{π}{2}$
设第三个角为γ,有以下三种情况:
i)α=γ,此时由于α+β+γ=π且α-β=-$\frac{π}{2}$
∴β=$\frac{2π}{3}$,α=$\frac{π}{6}$;
ii)β=γ,此时由于α+β+γ=π且α-β=-$\frac{π}{2}$
∴β=$\frac{π}{2}$,α=0,因此这种情况不可能;
iii)α=β,此时由于α-β=-$\frac{π}{2}$,因此这种情况是不可能的.
综上有,α=$\frac{π}{6}$,β=$\frac{2π}{3}$.
故选:A.
点评 本题考查三角函数的化简,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
15.执行如图的程序框图,输出的结果为( )
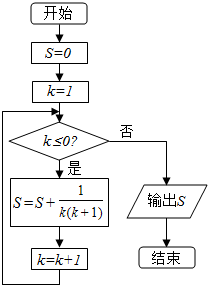

| A. | $\frac{8}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{10}{11}$ | D. | $\frac{9}{8}$ |
12.已知全集U={x∈N*|x<9 },集合∁U(A∪B)={1,3},A∩∁UB={2,4},则集合B等于( )
| A. | {1,3,5,6,7,8} | B. | {2,4,5,6,7,8} | C. | {5,6,7,8} | D. | {1,2,3,4} |
16.已知集合A={x|x2-2x-3<0},B={x|lnx>0},则A∩B=( )
| A. | {x|x>1} | B. | {x|x<3} | C. | {x|1<x<3} | D. | {x|-1<x<1} |
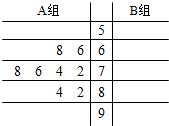 某班A、B两组各有8名学生,他们期中考试的美术成绩如下:
某班A、B两组各有8名学生,他们期中考试的美术成绩如下: