题目内容
【题目】已知函数![]() 有两个极值点
有两个极值点![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证:![]() ;
;
(3)求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析;(3)证明见解析
;(2)证明见解析;(3)证明见解析
【解析】
(1)求导化简得到![]() ,设
,设![]() ,画出函数图像得到答案.
,画出函数图像得到答案.
(2)构造函数![]() ,证明函数单调递增,得到
,证明函数单调递增,得到![]() ,代入化简得到答案.
,代入化简得到答案.
(3)根据题意![]() ,
,![]() ,两式相除得到:
,两式相除得到:![]() ,计算
,计算![]() ,
,![]() ,设
,设![]() ,证明
,证明![]() ,得到答案.
,得到答案.
(1)![]() ,
,![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,
,
函数在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() ,画出函数图像,如图所示:
,画出函数图像,如图所示:
根据图像知![]() .
.
(2)![]() 的两个根为
的两个根为![]() ,构造函数
,构造函数![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,故函数单调递增,且
,故函数单调递增,且![]() .
.
![]() ,即
,即![]() ,即
,即![]() ,
,
![]() ,
,![]() ,当
,当![]() 时,函数
时,函数![]() 单调递增,
单调递增,
故![]() ,即
,即![]() .
.
(3)根据题意![]() ,
,![]() ,两式相除得到:
,两式相除得到:![]() ,
,
设![]() ,
,![]() ,故
,故![]() ,解得
,解得![]() ,
,![]() ,
,
故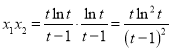 ,要证
,要证![]() ,即证
,即证![]() ,即
,即![]() .
.
设![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,且
,且![]() ,故
,故![]() 恒成立.
恒成立.
故![]() 单调递减,故
单调递减,故![]() 恒成立,得证.
恒成立,得证.
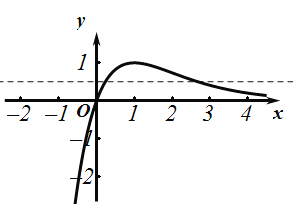

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】截至2019年,由新华社《瞭望东方周刊》与瞭望智库共同主办的"中国最具幸福感城市"调查推选活动已连续成功举办12年,累计推选出60余座幸福城市,全国约9亿多人次参与调查,使"城市幸福感"概念深入人心.为了便于对某城市的"城市幸福感"指数进行研究,现从该市抽取若干人进行调查,绘制成如下不完整的2×2列联表(数据单位:人).
男 | 女 | 总计 | |
非常幸福 | 11 | 15 | |
比较幸福 | 9 | ||
总计 | 30 |
(1)将列联表补充完整,并据此判断是否有90%的把握认为城市幸福感指数与性别有关;
(2)若感觉"非常幸福"记2分,"比较幸福"记1分,从上表男性中随机抽取3人,记3人得分之和为![]() ,求
,求![]() 的分布列,并根据分布列求
的分布列,并根据分布列求![]() 的概率
的概率
附: ,其中
,其中![]() .
.
| 0. 10 | 0. 05 | 0. 010 | 0.001 |
| 2.706 | 3.841 | 6. 635 | 10. 828 |
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(![]() )的检测数据,结果统计如下:
)的检测数据,结果统计如下:
|
|
|
|
|
|
| |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 | |
天数 | 6 | 14 | 18 | 27 | 25 | 20 |
(1)从空气质量指数属于![]() ,
,![]() 的天数中任取3天,求这3天中空气质量至少有2天为优的概率.
的天数中任取3天,求这3天中空气质量至少有2天为优的概率.
(2)已知某企业每天因空气质量造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() 的关系式为
的关系式为 假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为
假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
,9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
(i)记该企业9月每天因空气质量造成的经济损失为![]() 元,求
元,求![]() 的分布列;
的分布列;
(ii)试问该企业7月、8月、9月这三个月因空气质量造成的经济损失总额的数学期望是否会超过2.88万元?说明你的理由.