题目内容
【题目】已知![]() 的三边分别为
的三边分别为![]() 所对的角分别为
所对的角分别为![]() ,且三边满足
,且三边满足![]() ,已知
,已知![]() 的外接圆的面积为
的外接圆的面积为![]() ,设
,设![]() .则
.则![]() 的取值范围为______,函数
的取值范围为______,函数![]() 的最大值的取值范围为_______.
的最大值的取值范围为_______.
【答案】![]()
![]()
【解析】
化简已知等式结合余弦定理可得角B,然后利用基本不等式可得a+c的范围,再利用配方可得函数f(x)的最大值,由a+c的范围即得f(x)最大值的范围.
由![]() ,可知c(b+c)+a(a+b)=(a+b)(b+c),
,可知c(b+c)+a(a+b)=(a+b)(b+c),
化简得![]() ,由余弦定理可得cosB=
,由余弦定理可得cosB=![]() ,又B∈(0,π),B=
,又B∈(0,π),B=![]() ,
,
因为![]() ,解得R=
,解得R=![]() ,
,
由![]() ,解得b=3,
,解得b=3,
由余弦定理得![]() ,
,
由基本不等式可得![]() ,解得a+c≤6,根据两边之和大于第三边可得a+c>3,即a+c得取值范围是
,解得a+c≤6,根据两边之和大于第三边可得a+c>3,即a+c得取值范围是![]() ;
;
![]()
=-![]() +4(a+c)sinx+2=-2
+4(a+c)sinx+2=-2![]()
又-1≤sinx≤1,可知sinx=1时,函数f(x)的最大值为4(a+c),
函数![]() 的最大值的取值范围为
的最大值的取值范围为![]()
故答案为:(1)![]() (2)
(2)![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() (
(![]() ).对上述数据作了初步处理,得到相关的值如表:
).对上述数据作了初步处理,得到相关的值如表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() 若想在
若想在![]() 年达到年利润最大,请预测
年达到年利润最大,请预测![]() 年的宣传费用是多少万元?
年的宣传费用是多少万元?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为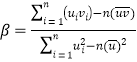 ,
,![]()