题目内容
(本题满分14分) 已知函数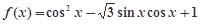 .
.
(1)求函数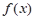 的单调递增区间;
的单调递增区间;
(2)若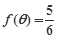 ,
,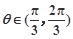 ,求
,求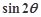 的值.
的值.
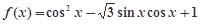 .
.(1)求函数
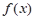 的单调递增区间;
的单调递增区间;(2)若
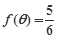 ,
,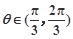 ,求
,求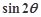 的值.
的值. (Ⅰ)函数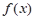 的单调递增区间是
的单调递增区间是 (
( ).
).
(Ⅱ)
 .
.
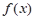 的单调递增区间是
的单调递增区间是 (
( ).
).(Ⅱ)

 .
.本试题主要是考查了三角函数图像与性质的综合运用。
(1)先化简函数为单一函数,利用二倍角公式来得到,进而结合函数的单调区间得到结论。
(2)在第一问的基础上,分析得到 的正弦值,然后利用凑角的思想得到求解。
的正弦值,然后利用凑角的思想得到求解。
解:(Ⅰ)

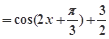 . …4分
. …4分
由 ,得
,得 (
( ).
).
∴函数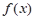 的单调递增区间是
的单调递增区间是 (
( ). …7分
). …7分
(Ⅱ)∵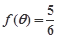 , ∴
, ∴ ,
,  .
.
∵ ,∴
,∴ ,
,  .…10分
.…10分
∴
 . …14分
. …14分
(1)先化简函数为单一函数,利用二倍角公式来得到,进而结合函数的单调区间得到结论。
(2)在第一问的基础上,分析得到
 的正弦值,然后利用凑角的思想得到求解。
的正弦值,然后利用凑角的思想得到求解。解:(Ⅰ)


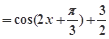 . …4分
. …4分由
 ,得
,得 (
( ).
).∴函数
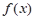 的单调递增区间是
的单调递增区间是 (
( ). …7分
). …7分(Ⅱ)∵
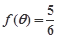 , ∴
, ∴ ,
,  .
. ∵
 ,∴
,∴ ,
,  .…10分
.…10分∴

 . …14分
. …14分
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 (其中
(其中 )的图象如图所示,则
)的图象如图所示,则





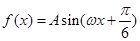 (其中
(其中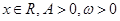 )的图象与
)的图象与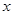 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为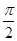 ,且图象上一个点为
,且图象上一个点为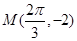 .
.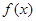 的解析式;
的解析式;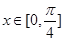 求函数
求函数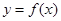 的图象向左平移
的图象向左平移 的结论中,错误的是( )
的结论中,错误的是( ) 的周期为
的周期为
 上是减函数
上是减函数
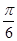 个单位得到函数
个单位得到函数 的图象.
的图象. 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的 解 析 式;
的 解 析 式; 中,角
中,角 的 对 边 分 别 是
的 对 边 分 别 是 ,若
,若 的 取 值 范 围.
的 取 值 范 围.
 ,设函数
,设函数

 的最小正周期及单调递增区间;(2)当
的最小正周期及单调递增区间;(2)当 时,求
时,求 为基底向量,且
为基底向量,且 若A、B、D三点共线,求实数k的值;
若A、B、D三点共线,求实数k的值;  一个周期内的简图,并指出该函数图象是由函数
一个周期内的简图,并指出该函数图象是由函数 的图象进行怎样的变换而得到的?
的图象进行怎样的变换而得到的?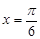 是函数
是函数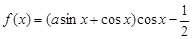 图象的一条对称轴.
图象的一条对称轴.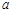 的值;
的值;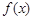 在
在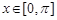 上的图象简图(不要求书写作图过程).
上的图象简图(不要求书写作图过程).
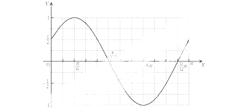
 的导函数
的导函数 的部分图像如图所示:图象与
的部分图像如图所示:图象与 轴交点
轴交点 ,与x轴正半轴的交点为A、C,B为图象的最低点 ,则函数
,与x轴正半轴的交点为A、C,B为图象的最低点 ,则函数
