题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为边长为2的菱形,∠DAB=60°,∠ADP=90°,面ADP⊥面ABCD,点F为棱PD的中点.
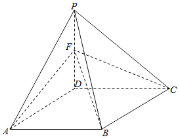
(1)在棱AB上是否存在一点E,使得AF∥面PCE,并说明理由;
(2)当二面角D﹣FC﹣B的余弦值为![]() 时,求直线PB与平面ABCD所成的角.
时,求直线PB与平面ABCD所成的角.
【答案】(1)见解析;(2)45°
【解析】
(1)点E为棱AB的中点取PC的中点Q,连结EQ、FQ,推导出四边形AEQF为平行四边形,从而AF∥EQ,由此能证明AF∥平面PEC.(2)推导出ED⊥CD,PD⊥AD,且从而PD⊥面ABCD,故以D为坐标原点建立空间坐标系,利用向量法能求出直线PB与平面ABCD所成的角.
(1)在棱AB上存在点E,使得AF∥面PCE,点E为棱AB的中点.
理由如下:取PC的中点Q,连结EQ、FQ,由题意,FQ∥DC且![]() ,AE∥CD且
,AE∥CD且![]() ,
,
故AE∥FQ且AE=FQ.所以,四边形AEQF为平行四边形.所以,AF∥EQ,又EQ平面PEC,AF平面PEC,
所以,AF∥平面PEC.
(2)由题意知△ABD为正三角形,所以ED⊥AB,亦即ED⊥CD,又∠ADP=90°,
所以PD⊥AD,且面ADP⊥面ABCD,面ADP∩面ABCD=AD,
所以PD⊥面ABCD,故以D为坐标原点建立如图空间坐标系,
设FD=a,则由题意知D(0,0,0),F(0,0,a),C(0,2,0),![]() ,
,
![]() ,
,![]() ,设平面FBC的法向量为
,设平面FBC的法向量为![]() ,
,
则由 得
得![]() ,令x=1,则
,令x=1,则![]() ,
,![]() ,
,
所以取![]() ,显然可取平面DFC的法向量
,显然可取平面DFC的法向量![]() ,
,
由题意: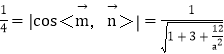 ,所以a=1.
,所以a=1.
由于PD⊥面ABCD,所以PB在平面ABCD内的射影为BD,
所以∠PBD为直线PB与平面ABCD所成的角,
易知在Rt△PBD中![]() ,从而∠PBD=45°,
,从而∠PBD=45°,
所以直线PB与平面ABCD所成的角为45°.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目

