题目内容
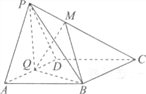
【题目】如图，在四棱锥
中，底面
是菱形，
为
的中点，
为
的中点．证明：直线
平面
.
【答案】证明见解析
【解析】
试题方法一，取OB的中点G，连接GN、GM。证明平面MNG∥平面OCD，从而可证得MN∥平面OCD。
方法二：取OD的中点P，连接MP、CP。可证得四边形MNCP为平行四边形，因此MN∥PC，由线面平行的判定定理可得MN∥平面OCD。
试题解析：
方法一：如图，取OB的中点G，连接GN、GM。
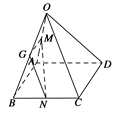
∵M为OA的中点，
∴MG∥AB.
∵AB∥CD，
∴MG∥CD.
∵MG
平面OCD，CD平面OCD，
∴MG∥平面OCD。
又G、N分别为OB、BC的中点，
∴GN∥OC。
∵GN平面OCD，OC平面OCD，
∴GN∥平面OCD。
又MG∩GN＝G，
∴平面MNG∥平面OCD。
∵MN平面MNG，
∴MN∥平面OCD。
方法二：如图，取OD的中点P，连接MP、CP。
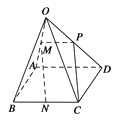
∵M为OA的中点，
∴
且
。
∵N为BC的中点，
∴
且
，
∴
且
，
∴四边形MNCP为平行四边形，
∴MN∥PC。
又∵MN平面OCD，PC平面OCD，
∴MN∥平面OCD.
练习册系列答案
相关题目
