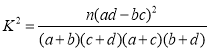题目内容
【题目】在平面直角坐标系xOy中,A(﹣2,0),B(2,0),P为不在x轴上的动点,直线PA,PB的斜率满足kPAkPB![]() .
.
(1)求动点P的轨迹Γ的方程;
(2)若M,N是轨迹Γ上两点,kMN=1,求△OMN面积的最大值.
【答案】(1)![]() (y≠0);(2)
(y≠0);(2)![]()
【解析】
(1)设P(x,y)为轨迹Γ上任意一点,根据kPAkPB![]() ,得到
,得到![]() ,化简即得解;
,化简即得解;
(2)设MN:y=x+b,联立得到韦达定理,利用弦长公式表示弦长|MN|,O到直线MN的距离,继而表示△OMN的面积,利用导数研究单调性,求最值即可.
(1)设P(x,y)为轨迹Γ上任意一点,则根据kPAkPB![]() .
.
即![]() ,
,
整理得动点P的轨迹Γ的方程为:![]() (y≠0);
(y≠0);
(2)设MN:y=x+b,联立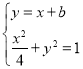 ,
,
整理得5x2+8bx+4b2﹣4=0,
△=5﹣b2>0,
设M(x1,y1),N(x2,y2),
则x1+x2![]() b,x1x2
b,x1x2![]() (b2﹣1),
(b2﹣1),
|MN|![]() |x1﹣x2|
|x1﹣x2|![]() ,
,
O到直线MN的距离d![]() ,
,
所以△OMN面积S![]() ,
,
设f(b)=5b2﹣b4,
则f′(b)=10b﹣4b3=0,
解得b=0或b=±![]() ,
,
又因为5﹣b2>0,
故b=0或b=±![]()
且S(0)=0,S(±![]() )
)![]() ,
,
故△OMN的面积S最大值为![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】甲乙两个班级均为 40 人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为 36 人,乙班及格人数为 24 人.
(1)根据以上数据建立一个2![]() 2的列联表;
2的列联表;
(2)试判断是否成绩与班级是否有关?
参考公式:![]() ;
;![]()
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |