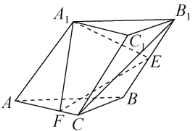
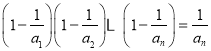题目内容
【题目】某工厂生产某款机器零件，因为要求精度比较高，所以需要对生产的一大批零件进行质量检测.首先由专家根据各种系数制定了质量指标值，从生产的大批零件中选取100件作为样本进行评估，根据评估结果作出如图所示的频率分布直方图.
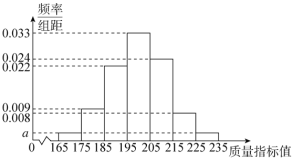
（1）（ⅰ）根据直方图求
及这100个零件的样本平均数
（同一组数据用该组数据区间的中点值表示）；
（ⅱ）以样本估计总体，经过专家研究，零件的质量指标值
，试估计10000件零件质量指标值在
内的件数；
（2）设每个零件利润为
元，质量指标值为
，利润与质量指标值之间满足函数关系
.假设同组中的每个数据用该组区间的中点值代替，试估算该批零件的平均利润.（结果四舍五入，保留整数）
参考数据：
，则
，
，
【答案】（1）（ⅰ）
，
；（ⅱ）8186；（2）182元.
【解析】
（1）（ⅰ）利用频率分布直方图的面积为
，求得
；再根据频率分布直方图求平均数即可；
（ⅱ）根据正态分布的概率计算，结合（1）中所求，即可求得质量指标值在
内的概率，进而结合总体数量求得结果；
（2）根据题意，结合利润计算的函数关系，即可容易求得.
（1）（ⅰ）由
，
解得.
（ⅱ）由题
，
所以
.
.
所以10000件零件质量指标值在内的件数约为8186.
（2）由题意得
该零件的平均利润为182元.
一本好题口算题卡系列答案
【题目】某地区2007年至2013年农村居民家庭人均纯收入y(单位：千元)的数据如下表：
年 份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程；
(2)利用(1)中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为：
＝
，
＝
－
．
